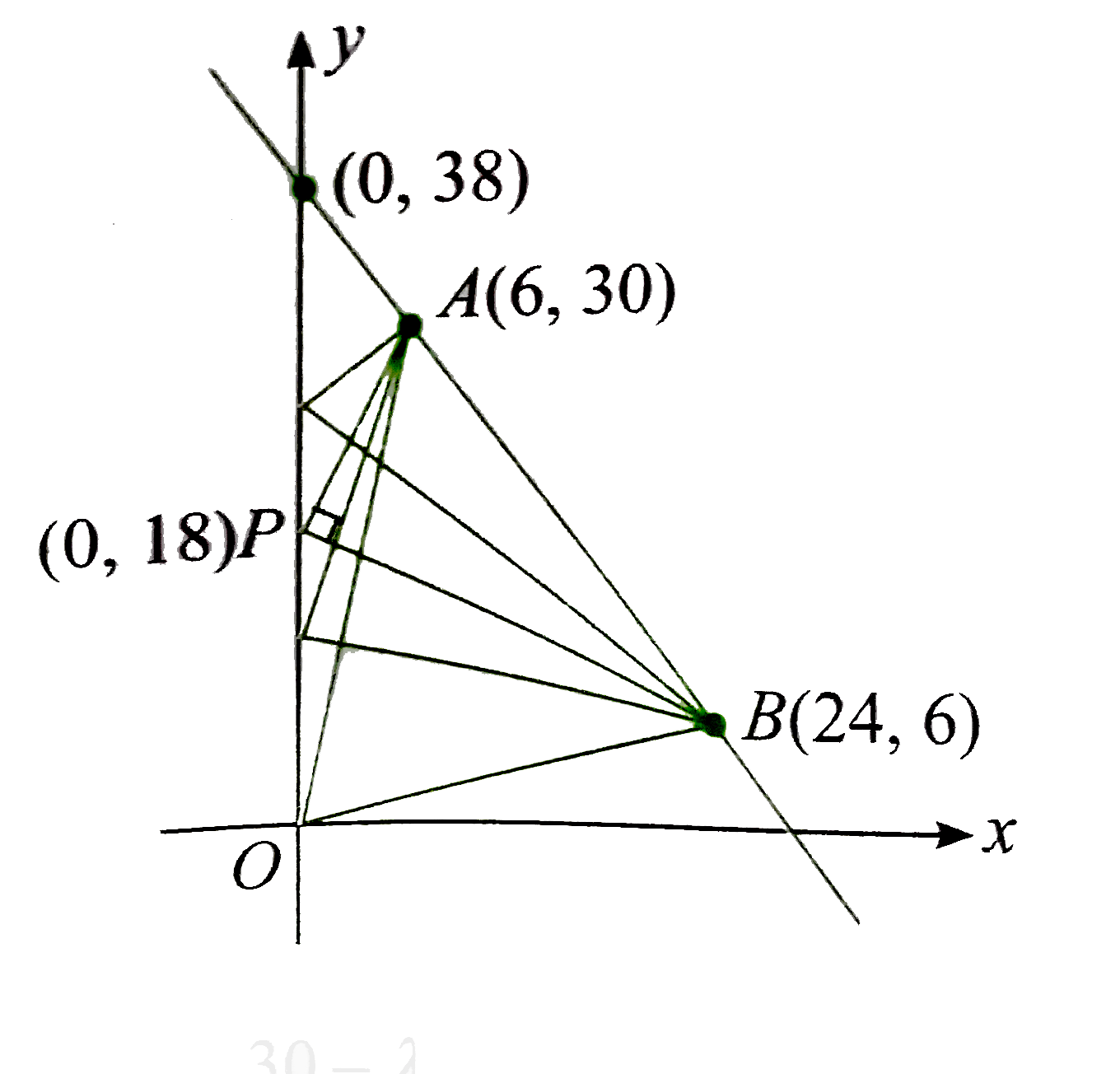
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point $P (0, λ)$ is a point on y-axis such that $0 < λ < 38 and point Q (0, λ)$ is a point on y-axis such that $λ > 38$ .
For all positions of pont Q, and AQB is maximum when point Q is

A

(0, 54)

B

(0, 58)

C

(0, 60)

D

(0, 1)

Text Solution

Verified by Experts

The correct Answer is:B

$Slope of A P is m_{1} = \frac{30 - λ}{6}$
$Slope of B P is m_{2} = \frac{6 - λ}{24}$
$tan θ = \frac{\frac{30 - λ}{6} - \frac{6 - λ}{24}}{1 + (\frac{30 - λ}{6}) (\frac{6 - λ}{24})}$
$= \frac{720 - 24 λ - 36 + 6 λ}{144 + 180 - 36 λ + λ^{2}}$
$= \frac{18 (38 - λ)}{324 - 36 λ + λ^{2}} = \frac{(38 - λ) 18}{{(λ - 18)}^{2}}$
$Clearly, for 0 < λ < 38 .$
Maximum value of $tan θ \to \infty for which θ = \frac{π}{2},$
$Now, \frac{d}{d λ} (tan θ) = \frac{18 (18 - λ) (λ - 58)}{{(λ - 18)}^{4}}$
$Clearly, λ = 58$ is point of maximum as derivative changes sign from $' +' to' -'$ .
So, point $Q \equiv (0, 58) when ∠ A Q B$ is maximum.

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point $P (0, λ)$ is a point on y-axis such that $0 < λ < 38 and point Q (0, λ)$ is a point on y-axis such that $λ > 38$ .
For all positions of pont P, angle APB is maximum when point P is
A(0, 12)
B(0, 15)
C(0, 18)
D(0, 21)
Question 2 - Select One
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point $P (0, λ)$ is a point on y-axis such that $0 < λ < 38 and point Q (0, λ)$ is a point on y-axis such that $λ > 38$ .
The maximum value of angle APB is
A $\frac{π}{3}$
B $\frac{π}{2}$
C $\frac{2 π}{3}$
D $\frac{3 π}{3}$
Question 3 - Select One
Let two points be $A (1, - 1)$ and $B (0, 2)$ . If a point P(x', y') be such that the area of $Δ P A B = 5$ sq. units and it lies on the line, $3 x + y - 4 λ = 0$ , then a value of $λ$ is:
A4
B1
C $- 3$
D3

CENGAGE-STRAIGHT LINES-Exercise (Comprehension)

Home
Ask Doubt
Profile