Consider the circle x2+y2−8x−18y+93=0 with the center C and a point P(2,5) out side it. From P a pair of tangents PQ and PR are drawn to the circle with S as mid point of QR. The line joining P to C intersects the given circle at A and B. Which of the following hold (s)
CP is the arithmetic mean of AP and BP
PR is the geometric mean of PS and PC
PS is the harmonic mean of PA and PB
The angle between the two tangents from P is tan−1(43)
The correct Answer is:A, B, C, D
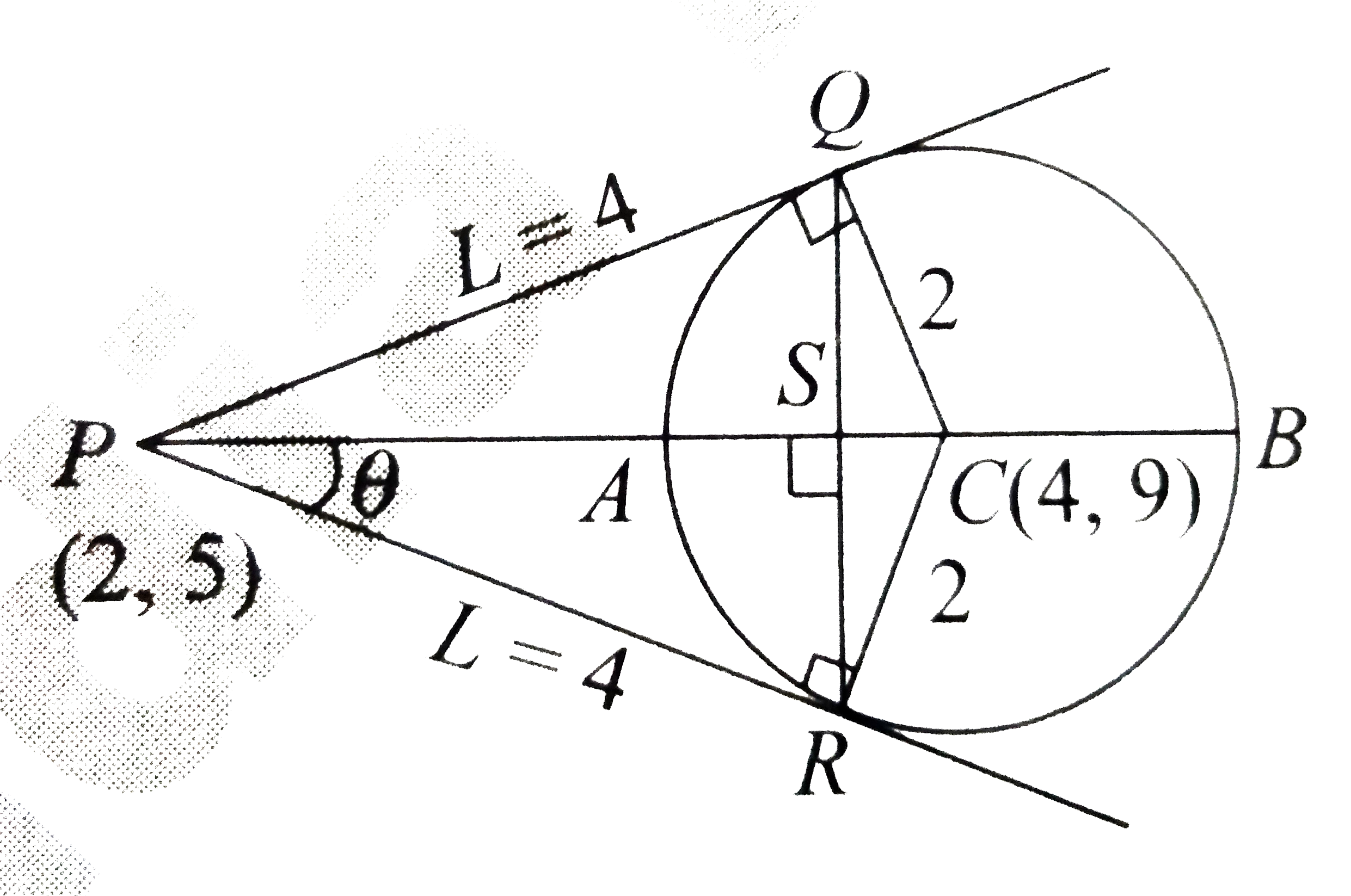
Radius =√16+81−93=2
CP=√20,AP=√20−2,BP=√20+2
⇒CP=AP+BP2
Thus, CP is the arithmetic mean of AP and BP
Now let, L=PR=√(PC)2−r2=√20−4=4=PQ
∴tanθ=24=12
Also, cosθ=PSPR
⇒PS=PRcosθ4.(2√5)=8√5
Harmonic mean between PA and PB
=2(√20−2)(√20+2)2√20=162√5=8√8=PS
Thus, PS is the harmonic mean of PA and PB.
(PS)(CP)=(8√5)(√20)=16=(PR)2
Thus, PR is the geometric mean of PS and CP.
Now, angle between the two tangents.
=2θ=2tan−1(12)=tan−1⎛⎝2.121−14⎞⎠=tan−1(43)
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
From the point P(2, 3) tangents PA,PB are drawn to the circle x2+y2−6x+8y−1=0. The equation to the line joining the mid points of PA and PB is
View SolutionLet P be a variable point. From P tangents PQ and PR are drawn to the circle x2+y2=b2 if QR always touch the parabola y2=4ax then locus ofP is
View Solution
Knowledge Check
From the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If C is the centre of the circle, then area of quadrilateral PQCR is
A450 sq unitsB15 sq unitsC50 sq unitsD75 sq unitsFrom the point P(16, 7) tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0. If c be the centre of the circle, then area of quadrilateral PQCR is
A450 sq unitB15 sq unitC50 sq unitD75 sq unitTangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
From the point P(16,7), tangents PQ and PR are drawn to the circle x2+y2−2x−4y−20=0 If C is the centre of the circle, then area of quadrilateral PQCR is
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View Solution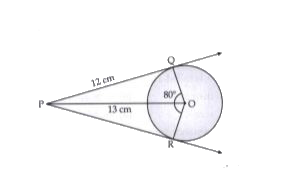
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
Find the radius of the circle.
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View SolutionTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
View Solution
