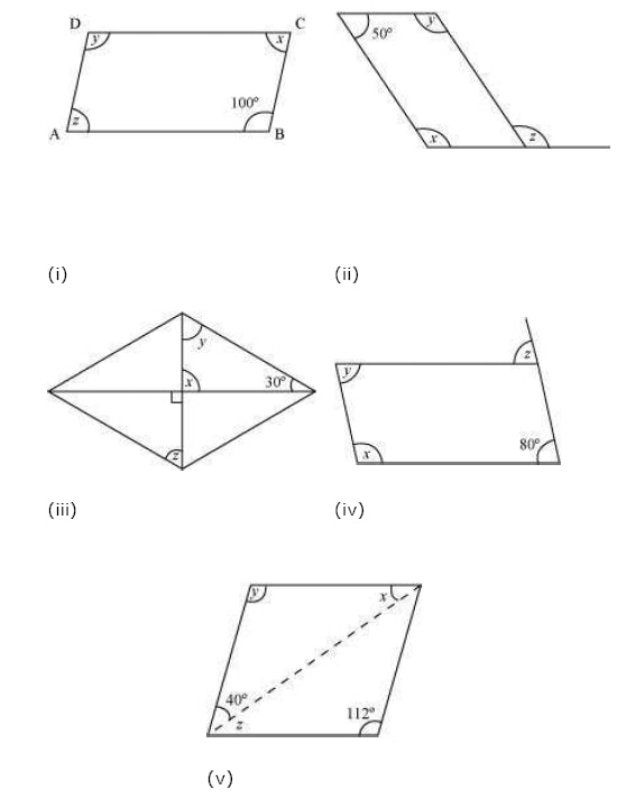
Consider the following parallelograms. Find the values of the unknowns .
Video Solution
Text Solution
(i)Since D is opposite to B.
So,
(Since oppositeanglesofparallelogram areequal)
(The adjacent angles in a parallelogram are supplementary
Therefore
[Since opposite angles of a parallelogram are equal]and adjacent angles are supplementary.]
Using this property, we cancalculate the measure of the unknown angles.]
Solution:]
(The adjacent angles in aparallelogramaresupplementary )]
(Since opposite angles of a parallelogram are equal)
(Corresponding angle
(iii)In a parallelogram, opposite angles are equal
and adjacent angles are supplementary.Using this property,
wecancalculate the measure of the unknown angles.
Solution
(Corresponding angles)
(since oppositeanglesofaparallelogramareequal
(Adjacentanglesaresupplementary
therefore
,,
(iv)In a parallelogram, opposite angles are equal and adjacent angles are
supplementary.
Using this property, we can
calculate the measure of the unknown angles.
(angle sum property of triangle)
(vertically opposite angles
(alternate interior angle)
(v )
(Alternate interior angle)
|
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBook:NCERTChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE 3.1
Explore 2 Videos
- UNDERSTANDING QUADRILATERALSBook:NCERTChapter:UNDERSTANDING QUADRILATERALSExercise:EXERCISE 3.2
Explore 6 Videos
- SQUARES AND SQUARE ROOTSBook:NCERTChapter:SQUARES AND SQUARE ROOTSExercise:EXERCISE 6.1
Explore 9 Videos
- VISUALISING SOLID SHAPESBook:NCERTChapter:VISUALISING SOLID SHAPESExercise:EXERCISE 10.3
Explore 8 Videos
Similar Questions
Consider the following parallelgorams. Find the value of the unknows x,y,z.
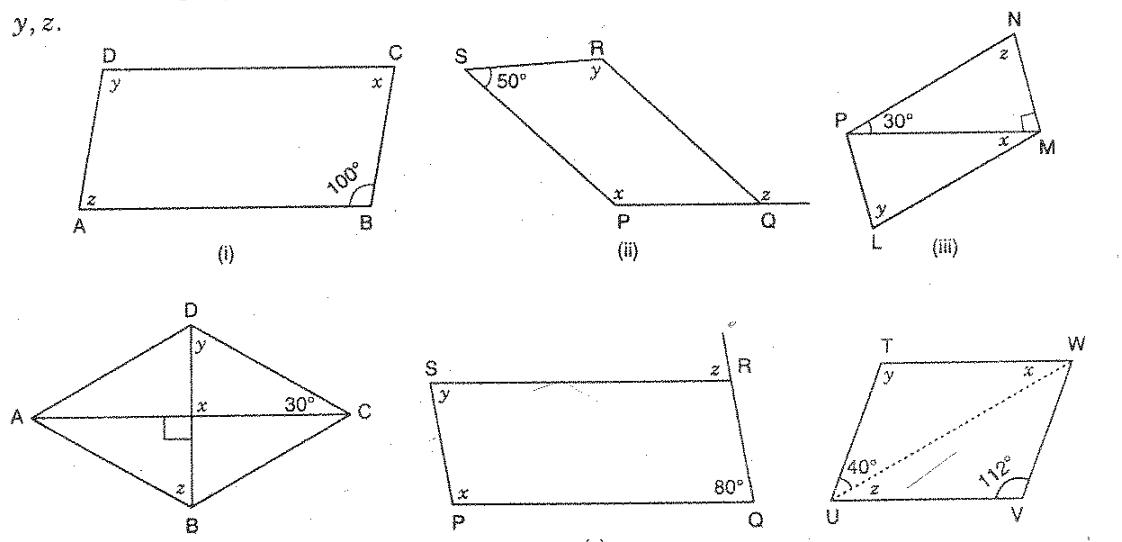
View SolutionThe following figures are parallelograms. Find the degree values of the unknowns x, y, z
View Solutionfind the value of x, y, z
View SolutionFind the value of x,y and z.
View SolutionFind the value of x, y and Z
View SolutionABCD is a parallelogram. Find the value of x, y and z.
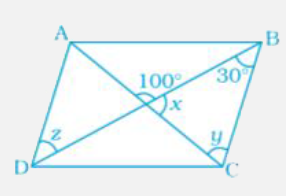
View SolutionIn Figure, BEST is a parallelogram. Find the values of x, y and z.
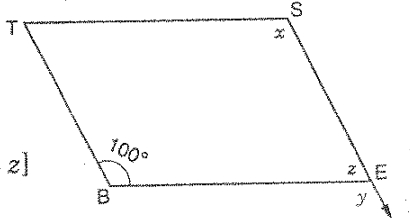
View SolutionConsider a parallelogram ABCD in the figure. Find the value of x.

View SolutionIf ABCD is a parallelogram, then find the values of x and y.
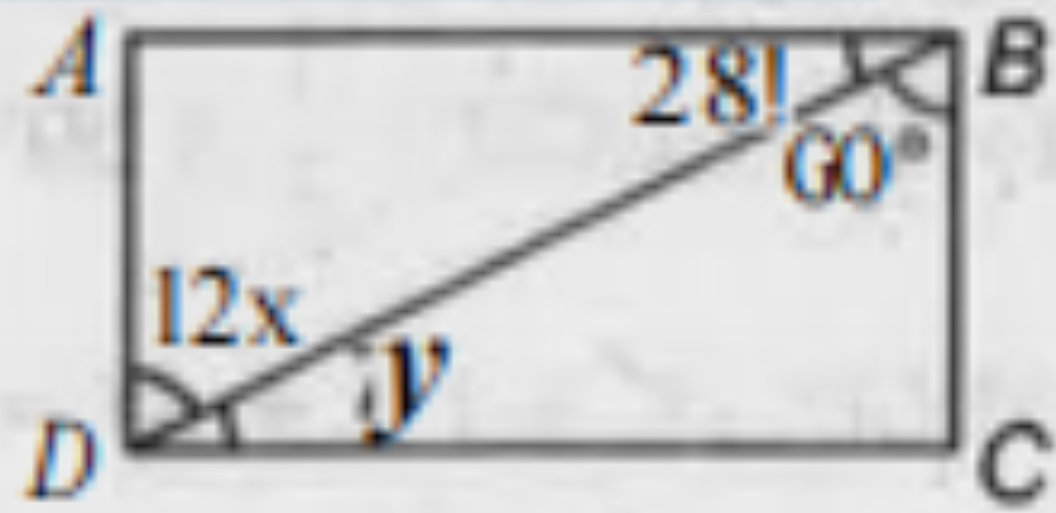
View SolutionIn the figure , ABCD is a parallelogram . Then find the value of x and y.

View Solution