Consider the sequence of natural numbers s0,s1,s2,... such that s0=3,s1=3andsn=3+sn−1sn−2, then
eπ2
e−π
eπ
e−π2
The correct Answer is:C
Since −1≤sinx≤1, the curve y=e−xsinx is bounded by the curve y=e−xandy=e−x.
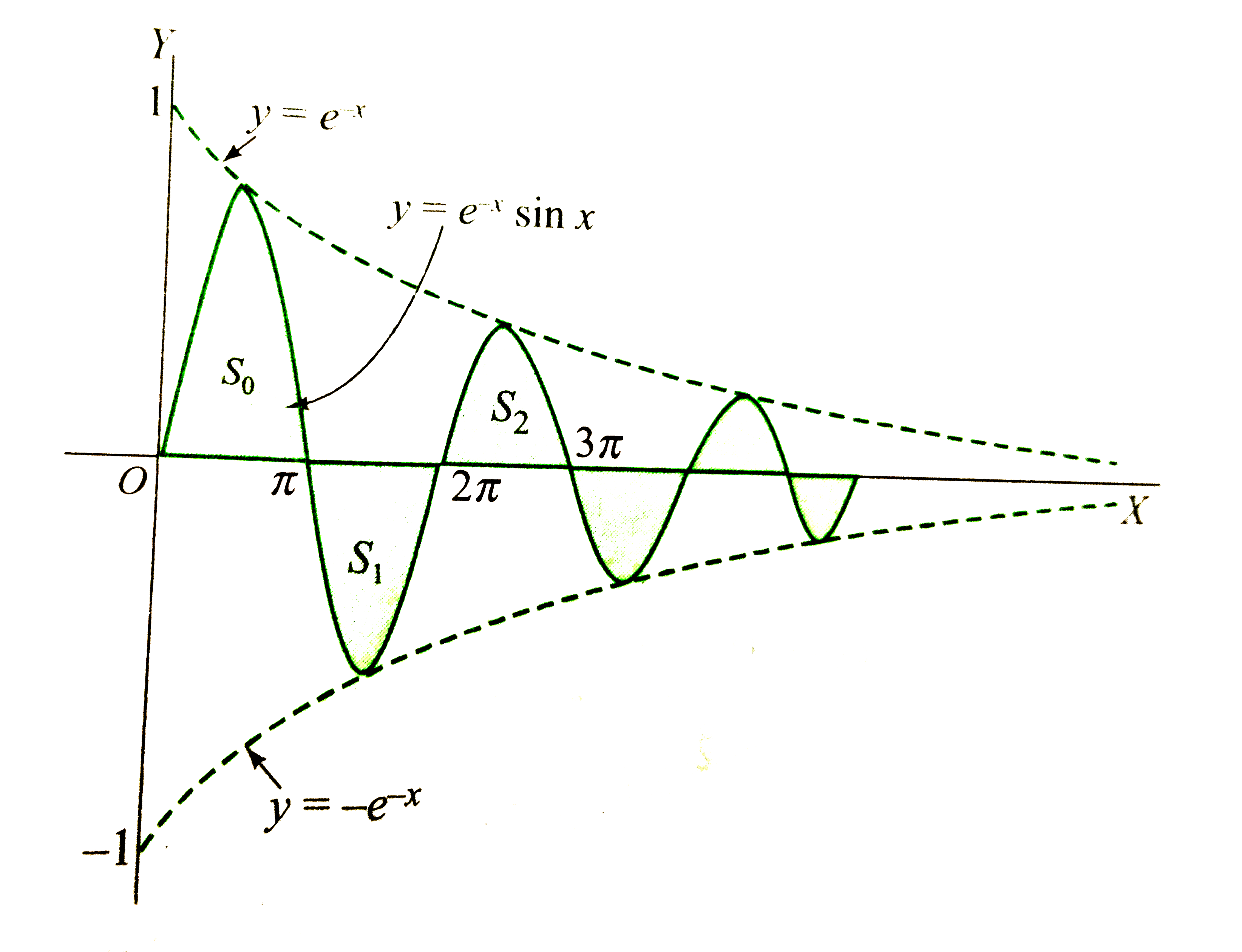
Also, the curve y=e−xsinx intersects the positive semi-axis OX at the points where sin x=0, where xn=nπ,n∈Z.
Also |yn|=|y coordinate in the half-wave Sn|
∴ Sn=(−1)n(n+1)π∫nπe−xsinxdx
=(−1)n+12[e−x(−sinx+cosx)](n+1)πnπ
=(−1)n+12[e−(n+1)x(−1)n+1−enπ(−1)n]
=e−nπ2(1+eπ)
⇒ Sn+1Sn=e−π
and S0=12(1+eπ).
Therefore, the sequence S0,S1,S2,... forms an infinite G.P. with common ratio e−π. we have
∞Σn=0Sn=12(1+eπ)1−e−π
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)
16 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
If S1,S2,S3 are the sums of first n natural numbers, their squares and cubes respectively, show that 9S22=S3(1+8S1).
View SolutionIf sum of n termsof a sequende is Sn then its nth term tn=Sn−Sn−1. This relation is vale for all n>−1 provided S0=0. But if S≠0, then the relation is valid ony for n≥2 and in hat cast t1 can be obtained by the relationt1=S1. Also if nth term of a sequence t1=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer thefollowing questions:If nth term of a sequence is n1+n2+n4 then the sum of its first n terms is (A) n2+n1+n+n2 (B) n2−n1+n+n2 (C) n2+n1−n+n2 (D) n2+n2(1+n+n2)
View Solution
Knowledge Check
For the Sn=3n2+5n sequence, the number 5456 is the ____th term
A153B932C707D909S= limn→∞n∑k=01√n2+k2
Adoes not existBexists and lies in the interval (0,1)Cexists and lies in the interval [1, 2)Dexists and lies in the interval [2, ∞)If N be the set of natural numbers is partitioned into groups S1=(1),S2=(2,3),S3=(4,5,6),... then the sum of the numbers in S50 is
A62525B57567C62505Dnone
If S_(n) denotes the sum of first 'n' natural numbers then s_(1)+S_(2)x+S_(3)x^(2)+.........+S_(n) x^(n-1)+......oo=(1-x)^(-n) then n is
View SolutionA sequence contains the terms S1,S2,S3,....Sn, where S2=2&Sn=Sn−1+2S2 What is the value of S18
View SolutionLet the sum of n, 2n, 3n terms of an A.P. be S1,S2and S3, respectively, show that S3=3(S2−S1).
View SolutionIn a G.P. if S1,S2&S3 denote respectively the sums of the first n terms , first 2 n terms and first 3 n terms , then prove that, S21+S22=S1(S2+S3).
View SolutionDefine a sequence {Sn} of real numbers by
Sn=n∑k=01√n2+k, for n≥1.
Then limn→∞Sn
View Solution
