Construct a triangle ABC in which AB=5.8cm, BC+CA=8.4 cm and ∠B=600
To construct triangle ABC with the given conditions AB=5.8cm, BC+CA=8.4cm, and ∠B=60∘, follow these steps:
1. Draw the Base:
- Draw a line segment AB measuring 5.8cm.
- Label the endpoints as A and B.
Hint: Use a ruler to ensure the line segment is straight and accurately measures 5.8cm.
2. Construct Angle B:
- At point B, construct an angle of 60∘.
- You can use a protractor for this step. Place the protractor's center at point B and mark 60∘.
Hint: Ensure the protractor is aligned correctly with line AB to get an accurate angle.
3. Draw Ray from B:
- Draw a ray BX along the 60∘ line. This ray will help in locating points C and D.
Hint: Extend the ray sufficiently to allow for the intersection with the arc later.
4. Mark the Length of BC + CA:
- Set your compass to 8.4cm.
- With the compass point on B, draw an arc that intersects the ray BX. Label the intersection point as D.
Hint: Make sure the compass is not too loose, as it can affect the accuracy of the arc.
5. Construct Perpendicular Bisector:
- To find point C, we need to construct the perpendicular bisector of segment AD.
- First, measure the distance AD and set the compass to more than half of this distance.
- With the compass point on A, draw an arc above and below the line segment AD.
- Without changing the compass width, repeat this from point D to create two intersection points.
- Draw a line through these intersection points. This is the perpendicular bisector.
Hint: Ensure you draw arcs that are large enough to intersect clearly.
6. Locate Point C:
- The intersection of the perpendicular bisector with ray BX gives you point C.
Hint: Label point C clearlytoavoidconfusionwithotherpoints.</p><p>7.<strong>CompletetheTriangle</strong>:−Finally,connectpoints A and C withastraightlineandalsoconnectpoints B and C .</p><p><strong>Hint</strong>:Usearulertoensurethelinesarestraightandaccuratelydrawn.</p><p><strong>Conclusion:</strong>Youhavenowconstructedtriangle ABC withthespecifiedconditions.</p><p><strong>Justification:</strong>− AB = 5.8 \, \text{cm} isgiven.− \angle B = 60^\circ isconstructed.−Thepoint C liesontheperpendicularbisectorof AD ,ensuringthat BC + CA = 8.4 \, \text{cm} .
- Draw a line segment AB measuring 5.8cm.
- Label the endpoints as A and B.
- At point B, construct an angle of 60∘.
- You can use a protractor for this step. Place the protractor's center at point B and mark 60∘.
- Draw a ray BX along the 60∘ line. This ray will help in locating points C and D.
- Set your compass to 8.4cm.
- With the compass point on B, draw an arc that intersects the ray BX. Label the intersection point as D.
- To find point C, we need to construct the perpendicular bisector of segment AD.
- First, measure the distance AD and set the compass to more than half of this distance.
- With the compass point on A, draw an arc above and below the line segment AD.
- Without changing the compass width, repeat this from point D to create two intersection points.
- Draw a line through these intersection points. This is the perpendicular bisector.
- The intersection of the perpendicular bisector with ray BX gives you point C.
Topper's Solved these Questions
Similar Questions
Draw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
View SolutionIn which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
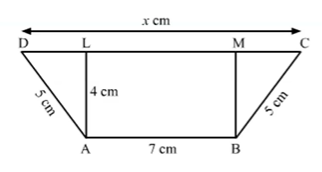
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AD=5.6cm , BC=6cm and BD=3.2cm , find AC . (ii) If AB=10cm , AC=6cm and BC=12cm , find BD and DC .
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=12 cm, AD=8 cm, AE=12 cm and AC=18 cm . (ii) AB=5.6 cm, AD=1.4 cm, AC=7.2 cm and AE=1.8 cm
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View Solution
