In Figure, $A B = A C . B E$ and $C F$ are respectively the bisectors of $∠ B$ and $∠ C$ . Prove that $E B C = F C B .$ Figure

Video Solution

|

Answer

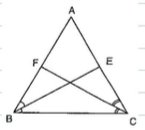
Step by step video & image solution for In Figure, A B=A CdotB E and C F are respectively the bisectors of /_B and /_C . Prove that E B C=F C Bdot Figure by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS CONGRUENCE OF TRIANGLES

Topper's Solved these Questions

Similar Questions

In Figure, $A B = A C . B E$ and $C F$ are respectively the bisectors of $∠ B$ and $∠ C$ . Prove that $E B C = F C B .$ Figure

View Solution
In Fig. 4.102 (i) and (ii) , if $C D$ and $G H$ $(D a n d H$ lie on $A B$ and $F E$ ) are respectively bisectors of $∠ A C B$ and $∠ E G F$ and $A B C ~ F E G$ , prove that (FIGURE) $D C A ~ H G F$ (ii) $\frac{C D}{G H} = \frac{A C}{F G}$ (iii) $D C B ~ H G E$
View Solution
In figure $A B = A C a n d C P ∣ ∣ B A$ and $A P$ is the bisector of exterior $∠ C A D$ of $A B C$ . Prove that $∠ P A C = ∠ B C A$ (ii) $A B C P$ is a parallelogram
View Solution
In Fig. 4.103, $C D$ and $G H$ are respectively the medians of $A B C$ and $E F G$ . If $A B C ~ F E G$ , prove that (FIGURE) $A D C ~ F H G$ (ii) $\frac{C D}{G H} = \frac{A B}{F E}$ (iii) $C D B ~ G H E$
View Solution
$A B$ and $C D$ are two parallel lines. $P Q$ cuts $A B a n d C D$ at $E a n d F$ respectively. $E L$ is the bisector of $∠ F E B .$ If $∠ L E B = 35^{0},$ then $∠ C F Q$ will be $55^{0}$ (b) $70^{0}$ (c) $110^{0}$ (d) $130^{0}$
View Solution
In Figure, $A B C$ is an isosceles triangle in which $A B = A C . C P p a r e l \leq l A B$ and $A P$ is the bisector of exterior $∠ C A D$ of $A B C$ . Prove that $∠ P A C = ∠ B C A$ and (ii) $A B C P$ is a parallelogram.

View Solution
In Figure, it is given that $A B = B C$ and $A D = E C$ . Prove that $A B E ≅ C B D$

View Solution
In Figure, it is given that $A B = E F, B C = D E, A B ⊥ B D$ and $F E ⊥ C E .$ Prove that $A B D ≅ F E C .$

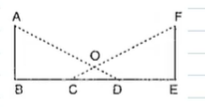
View Solution
In Figure, $B D$ and $C E$ are two altitudes of a $A B C$ such that $B D = C E .$ Prove that $A B C$ is isosceles.

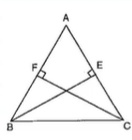
View Solution
In Figure, it is given that $A E = A D$ and $B D = C E .$ Prove that $A E B ≅ A D C$

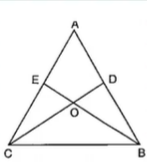
View Solution

RD SHARMA-CONGRUENT TRIANGLE -All Questions

Home
Ask Doubt
Profile

In Figure, AB=AC.BE and CF are respectively the bisectors of ∠B and ∠C . Prove that EBC=FCB. Figure

Topper's Solved these Questions

Similar Questions

RD SHARMA-CONGRUENT TRIANGLE -All Questions

In Figure, $A B = A C . B E$ and $C F$ are respectively the bisectors of $∠ B$ and $∠ C$ . Prove that $E B C = F C B .$ Figure