Construct a triangle ABC in which BC=5.7 cm, ∠B=450, AB−AC=3cm
1. Draw a line segment of base BC = 8 cm.
2. Measure and draw ∠B=45⋅ and extend the ray BX.
3. Using a compass and measure AB-AC = 3.5 cm.
4. Assume B as a center and draw an arc at the point be D on the ray BX
5. Join DC and now draw the perpendicular bisector of the line CD and the intersection point is assumed as A.
7. Join AC
8. Hence, ABC is the required triangle.
Topper's Solved these Questions
Similar Questions
In which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionDraw a triangle ABC with AB=6 cm, BC=7 cm and CA=8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
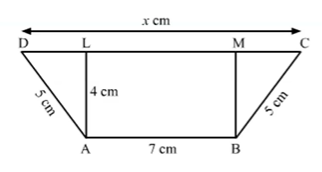
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
 View Solution
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If BD=2.5cm, AB=5cm and AC=4.2cm , find DC . (ii) If BD=2cm, AB=5cm and DC=3cm, find AC . (iii) If AB=3.5cm , AC=4.2cm and DC=2.8cm , find BD .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AD=5.6cm , BC=6cm and BD=3.2cm , find AC . (ii) If AB=10cm , AC=6cm and BC=12cm , find BD and DC .
View SolutionTriangle ABC is right angled at A.AD is perpendicular to BC. If AB=5 cm, BC=13 cm and AC=12 cm. Find the area of ABC. Also, find the length of AD.
View SolutionIn a ABC , AD is the bisector of ∠BAC . If AB=6cm , AC=5cm and BD=3cm , then DC= 11.3cm (b) 2.5cm (c) 3:5cm (d) None of these
View SolutionABC is a triangle and PQ is a straight line meeting AB in P and AC in Q . If AP=1cm , PB=3cm , AQ=1.5cm , QC=4.5m , prove that area of APQ is one-sixteenth of the area of ABC .
View Solution

