Construct an equilateral triangle whose altitude is 4 cm.
To construct an equilateral triangle whose altitude is 4 cm, follow these steps:
1. Draw the Altitude:
- Start by drawing a vertical line segment AD that measures 4 cm. This line represents the altitude of the equilateral triangle.
2. Mark the Midpoint:
- Let A be the top point of the altitude. Mark the point D at the bottom of the altitude. The midpoint of AD will be point B.
3. Construct the Base:
- Since the altitude bisects the base of the triangle, the length of the base BC can be calculated using the Pythagorean theorem. In an equilateral triangle, the relationship between the altitude h and the side s is given by:
h=√32s
- Rearranging gives:
s=2h√3=2×4√3=8√3≈4.62 cm
4. Construct Angles:
- At point A, construct two angles of 60∘ on either side of the altitude AD. You can do this using a protractor or a compass.
5. Draw the Base:
- From point A, draw lines AB and AC such that both angles ∠BAD and ∠CAD are 60∘. Extend these lines until they intersect at point C and point B.
6. Complete the Triangle:
- Connect points B and C to form the equilateral triangle ABC.
Final Triangle:
- The triangle ABC is your required equilateral triangle with an altitude of 4 cm.
- Start by drawing a vertical line segment AD that measures 4 cm. This line represents the altitude of the equilateral triangle.
- Let A be the top point of the altitude. Mark the point D at the bottom of the altitude. The midpoint of AD will be point B.
- Since the altitude bisects the base of the triangle, the length of the base BC can be calculated using the Pythagorean theorem. In an equilateral triangle, the relationship between the altitude h and the side s is given by:
h=√32s
- Rearranging gives:
s=2h√3=2×4√3=8√3≈4.62 cm
- At point A, construct two angles of 60∘ on either side of the altitude AD. You can do this using a protractor or a compass.
- From point A, draw lines AB and AC such that both angles ∠BAD and ∠CAD are 60∘. Extend these lines until they intersect at point C and point B.
- Connect points B and C to form the equilateral triangle ABC.
- The triangle ABC is your required equilateral triangle with an altitude of 4 cm.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE36videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise11videos
HERONS'S FORMULA
Similar Questions
Construct an equilateral triangle whose side is 5 cm.
View SolutionConstruct an equilateral ΔABC whose altitude is 4cm. Also construct a triangle similar to ΔABC with scale factor 34.
View SolutionAn equilateral triangle if its altitude is 3.2 cm.
View SolutionConstruct on equilateral triangle each of whose sides is of length 4.6cm.
View SolutionThe equation of a circle with the origin as the centre and passing through the vertices of an equilateral triangle whose altitude is of length 3 units is
View SolutionConstruct an equilateral triangle ABC with side 6 cm. Draw a circle circumscribing the triangle ABC.
View SolutionFind the area of an equilateral triangle whose side is a cm.
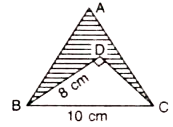
View SolutionThe given figure shows an equilateral triangle ABC whose each side is 10 cm and a right-angled triangle BDC whose side BD = 8 cm and ∠D=90∘. Find the area of the shaded portion.
 View Solution
View SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionFind the area of an equilateral triangle, whose one side is a cm.
View Solution

