An equilateral triangle if its altitude is 3.2 cm.
Video Solution
Text Solution
Steps of construction :
1. Draw a line l.
Mark any point D on the line l.
3. At point D, draw →DX⊥l and cut DA = 3.2 cm from →DX.
4. At the point A, construct AB and AC which meets the l at points B and C respectively such that
∠=30∘ and ∠DAC=30∘
Then, ΔABC is the required equilateral triangle
because ∠ABC=180∘−(90∘+30∘)=60∘.
∠ACB=180∘−(90∘+30∘)=60∘.
and ∠BAC=30∘+30∘=60∘
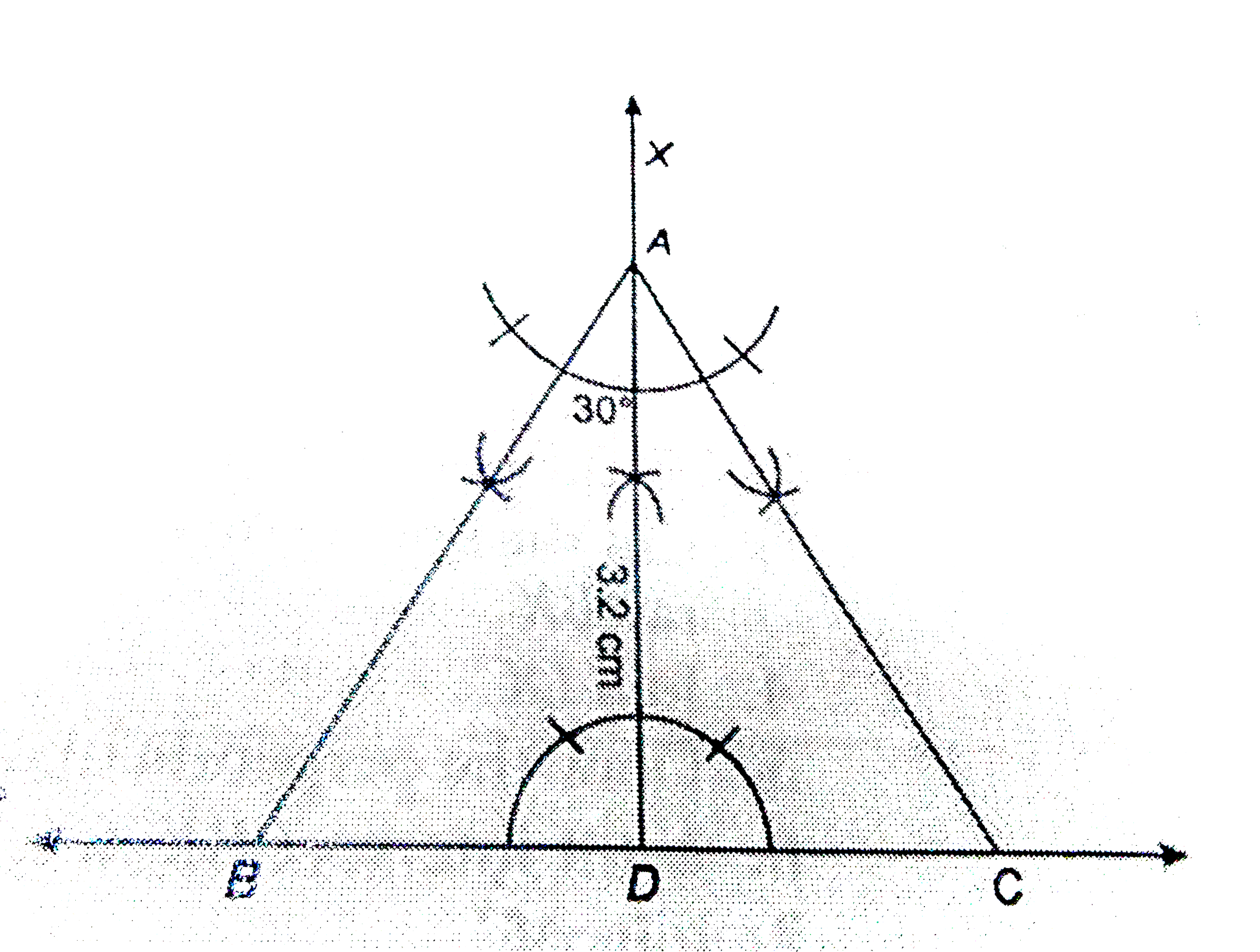
|
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
Similar Questions
Construct an equilateral triangle whose altitude is 4 cm.
View SolutionFind the perimeter of an equilateral triangle of side 13 cm.
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionFind the area of an equilateral triangle whose side is a cm.
View SolutionConstruct an equilateral triangle whose side is 5 cm.
View SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionFind the area of an equilateral triangle having altitude h cm.
View SolutionThe area of an equilateral triangle with side 2√3 cm is
View SolutionThe equation of a circle with the origin as the centre and passing through the vertices of an equilateral triangle whose altitude is of length 3 units is
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View Solution
