Corner points of fealible region of inequalities gives
an optiomal solution of L.P.P.
an objective function
the constraints.
the linear assumption.
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
The corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
View SolutionThe optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
View Solution
Knowledge Check
One of the corner points of the feasible region of inequalities gives
AOptimal solution of LPPBObjective functionCConstraintsDLinear assumptionsThe Corner points of feasible region for the inequations , x+y≤5,x+2y≤6,x≥0,y≥0 are
A(0,3),(5,0),(0,5),(6,0)B(0,3),(5,0),(4,1),(0,0)C(0,0),(1,4),(5,0),(0,3)D(3,0),(0,5)(0,0),(4,1)If the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101
The optimal value of the objective function is attained at the points A)Given by intersection of inequations with the axes only B)Given by intersection of inequations with the axes only C)Given by corner points of the feasible region D)None of these
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
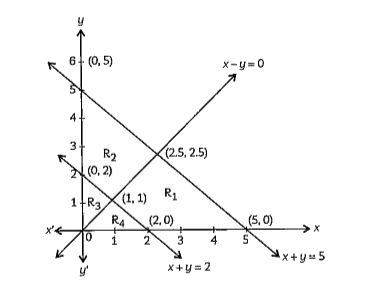
View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View Solutionthe corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
View SolutionThe corner points of the feasible region of a system of linear inequations are (0, 0), (5, 0), (6,5), (6, 8), (4, 10) and (0,8). If Z = 3x - 4y, then the minimum value of Z occurs at:
View Solution
