D and E are the mid-points of the side AB and AC, respectively, of ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is
A
B
AE=EF
C
DE=EF
D
Video Solution
Text Solution
The correct Answer is:C
In ADE and CFE, suppose DE=EF
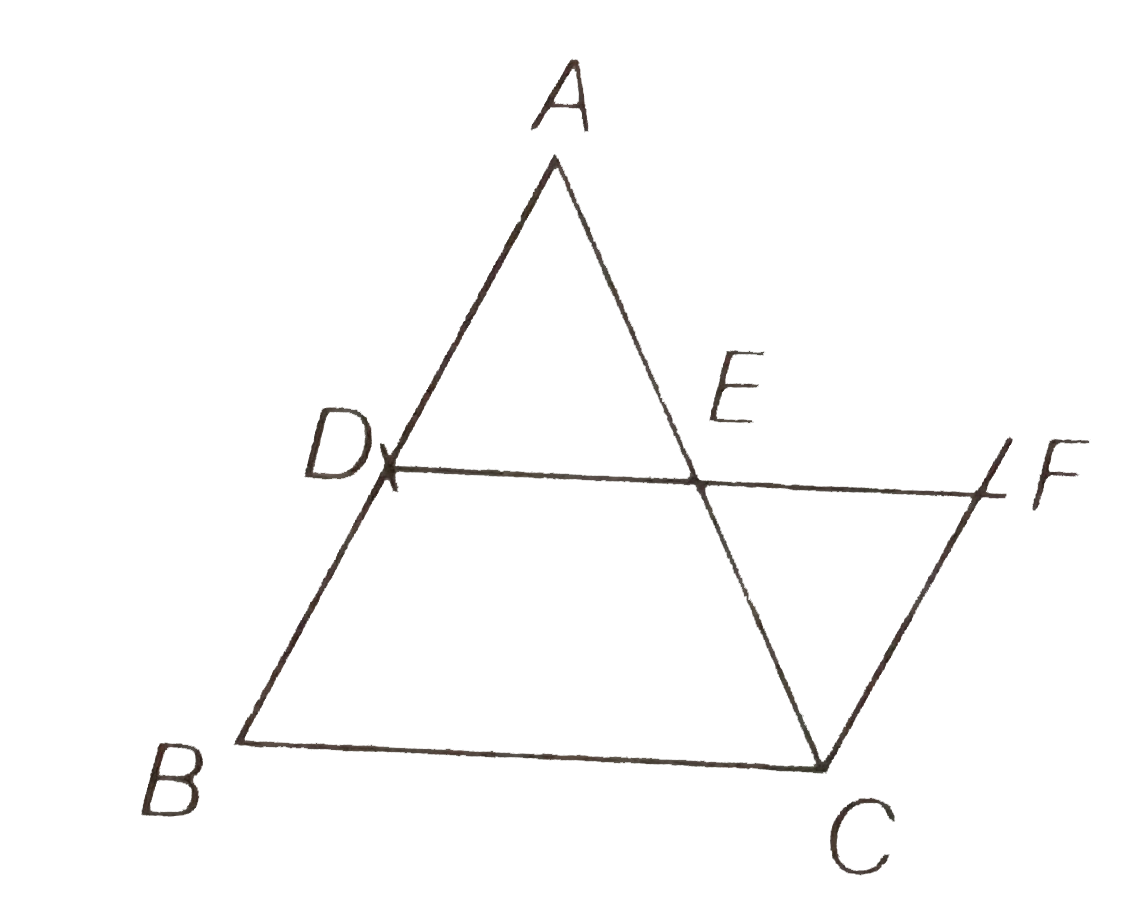
Now, AE=CE [since, E is the mid-point of AC]
Suppose DE=EF
and [vertically opposite angles]
[by SAS congruence rule]
[by CPCT rule] ltBrgt and [by CPCT]
Hence, [since, alternate interior angles are equal]
Therefore, we need an additional information which is DE=EF
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
Aa4−b4Ba2−b2Cb4−a4Db2−a2In a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CFLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of these
D and E , are the mid-points of AB and AC of ΔABC,BC is produced to any point P. DE, DP and EP are joined, then ΔPED is equal to ?
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
View Solution
