D,E,F are three points on the sides BC,CA,AB, respectively, such that ∠ADB=∠BEC=∠CFA=θ. A′,B'C' are the points of intersections of the lines AD,BE,CF inside the triangle. Show that are of A′B′C′=4cos2θ, where is the area of ABC.Solution in Tamil
From ΔAB'CAB'sin(π−(A+θ))=ACsin(π−B)

⇒AB'=2Rsin(A+θ)
From ΔAC'B,AC'sin(θ−A)=ABsin(π−C)
⇒AC'=2Rsin(θ−A)
∴B'C'=2R(sin(A+θ)−sin(θ−A))
=4RcosθsinA=2acosθ
Similarly, C'A'=2bcosθ
∴ Area of ΔA'B'C'=12(B'C')(A'C')sin∠B'C'A'
=12(2acosθ)(2bcosθ)sinC
=4cos2θ×Δ
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.2
8 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
15 Videos
Similar Questions
Find the value of a2+b2+c2R2 in any right-angled triangle.
View SolutionIf the sides of a triangle are a, b and √a2+ab+b2, then find the greatest angle
View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionIf f(x)<0, x∈(a,b) then at the point C(c, f(c)) on y=f(x) for whichF(c) is a maximum, f′(c) is given by a.f′(c)=f(b)−f(a)b−1 b. f′(c)=f(b)−f(a)a−b c.f′(c)=2(f(b)−f(a))b−a d. f′(c)=0
View SolutionD, E and F are the points on sides BC, CA and AB respectively of ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C . If AB=5cm, BC=8cm and CA=4cm , determine AF, CE and BD .
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
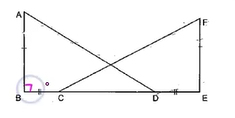
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
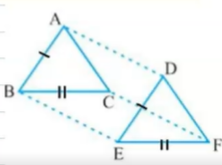
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
View SolutionThe sides BC,CA and AB of a triangle ABC, are produced in order, forming exterior angles ∠ACD,∠BAE and ∠CBF . Show that ∠ACD+∠BAE+∠CBF=3600
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DF⋅EF=FB⋅FA.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DE∣∣BC.
View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
View SolutionD, E and F are the points on sides BC, CA and AB respectively of ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C . If AB=5cm, BC=8cm and CA=4cm , determine AF, CE and BD .
View Solution
