Define the feasible region.
Video Solution
|
Answer
Step by step video & image solution for Define the feasible region. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise - 12.1
10 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise 12.2
11 Videos
- LINEAR PROGRAMMING BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 (C ) (True/False Questions)
5 Videos
- INVERSE - TRIGONOMETRIC FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)
11 Videos
- MATRICESBOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)
12 Videos
Similar Questions
Knowledge Check
The point which does not lie in the feasible region of 2x+3y<18 is :
A(9, 0)B(0, 0)C(4, 1)D(1, 5)In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
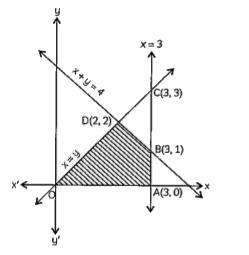 AOBBCCDD
AOBBCCDDThe maximum or minimum of the objective funtion occurs only at the corner points of the feasible region. This theorem is known as fundamental theorem of
AAlgebraBArithmeticCCalculusDExtreme point
Define the feasible solution.
View SolutionThe shaded part of the given figure indicates the feasible region

Then the constraints are
View SolutionThe shaded part of the given figure indicates the feasible region

Then the constraints are
View SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z=3x+9y maximum?
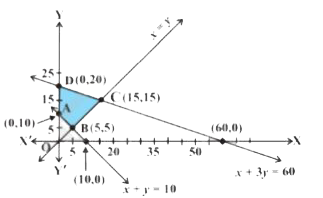
View SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum?
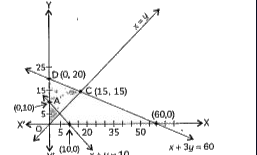
View Solution
