Define the feasible region.
Video Solution
|
Answer
Step by step video & image solution for Define the feasible region. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise - 12.110videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Exercise 12.211videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - EXERCISE 12 (C ) (True/False Questions)5videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)11videos
INVERSE - TRIGONOMETRIC FUNCTIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)12videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
The point which does not lie in the feasible region of 2x+3y<18 is :
A(9, 0)B(0, 0)C(4, 1)D(1, 5) - Question 2 - Select One
In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:
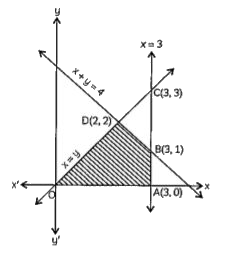AOBBCCDD - Question 3 - Select One
In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
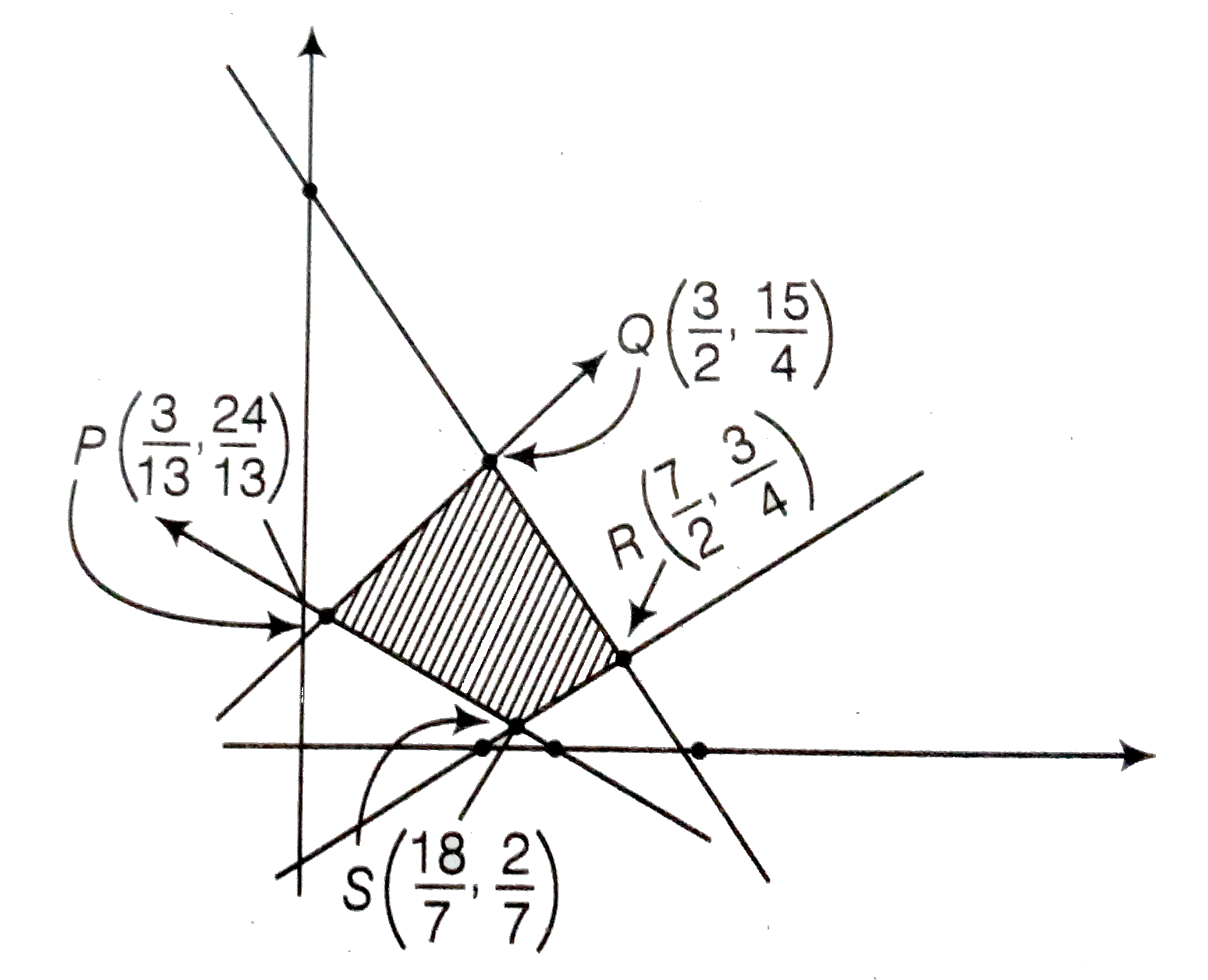Amaximum = 7 minimum = 479Bmaximum = 9 minimum = 317Cmaximum = 10 minimum = 345Dmaximum = 8 minimum = 547
Define the feasible solution.
View SolutionThe shaded part of the given figure indicates the feasible region
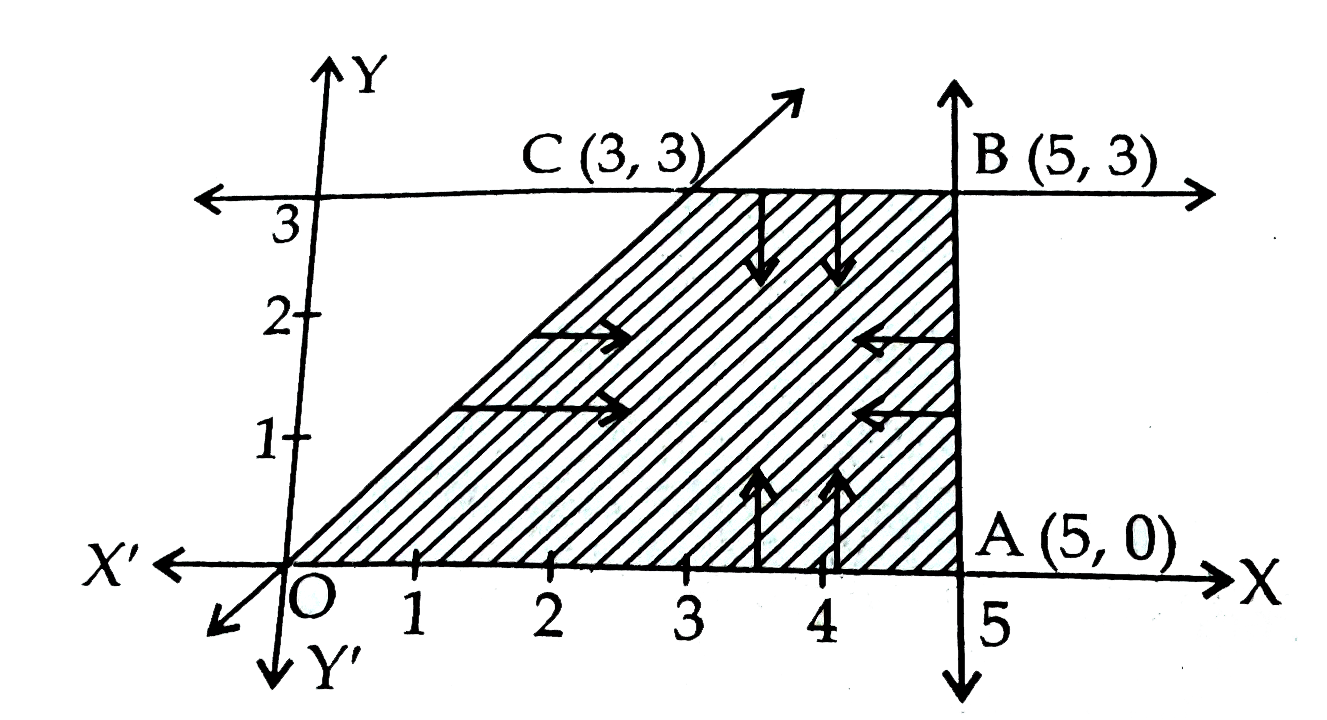
Then the constraints areView SolutionThe shaded part of the given figure indicates the feasible region
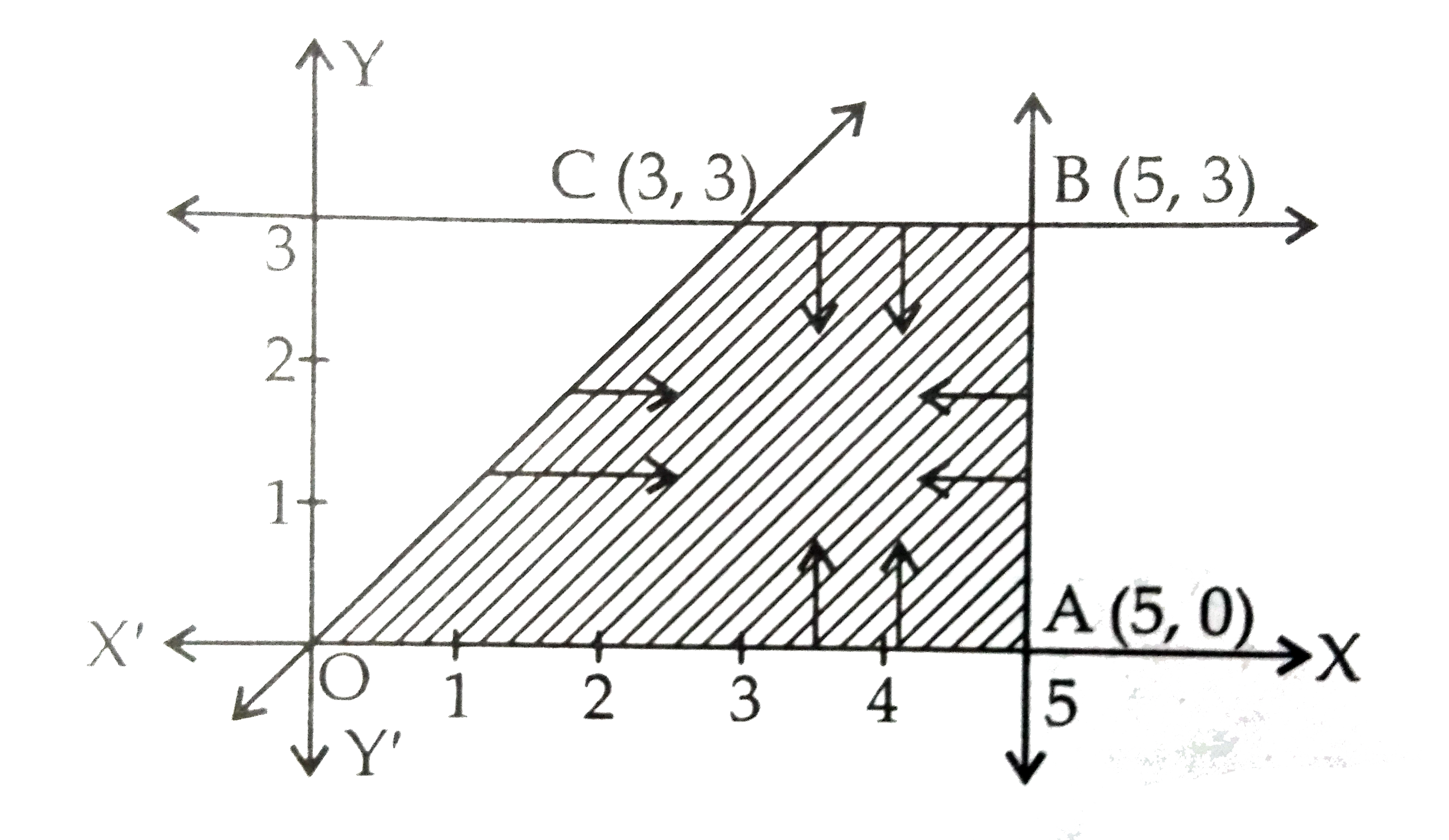
Then the constraints areView SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum?
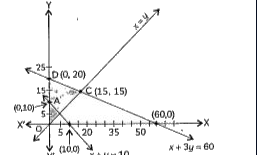
View SolutionBased on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z=3x+9y maximum?
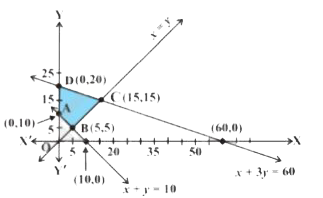
View Solution