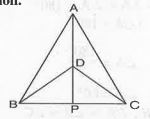
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
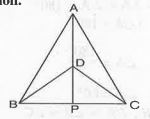 ).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.Solution in Punjabi
).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.Solution in Punjabi
Step by step video & image solution for DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig. ).If AD is extended to intersect BC at P, show that AP bisects angleA as well as angleD. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SWAN PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 7.46videos
TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 7.54videos
TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 7.210videos
TRIANGLES
- BOOK - SWAN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Objective Type Questions (Fill in the Blanks )7videos
SURFACE AREAS AND VOLUMES
Similar Questions
Show that in a right angled triangle, the hypotenuse is the longest side.
 09:03View Solution
09:03View SolutionABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
04:23View SolutionIn an isosclees triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O show that : OB=OC.
07:03View SolutionTotal surface area of a cone = ..............
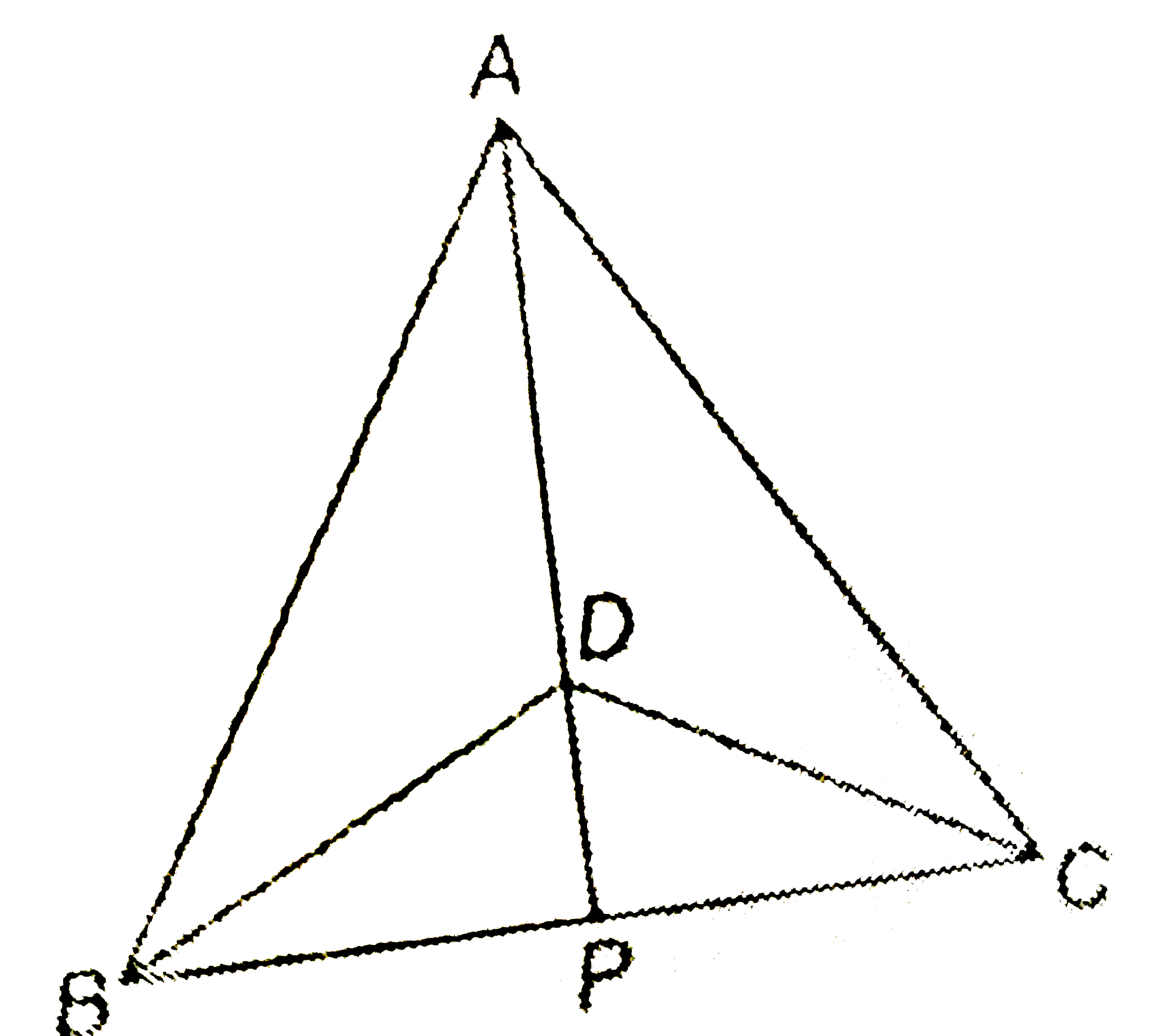
05:08View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
 03:10View Solution
03:10View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
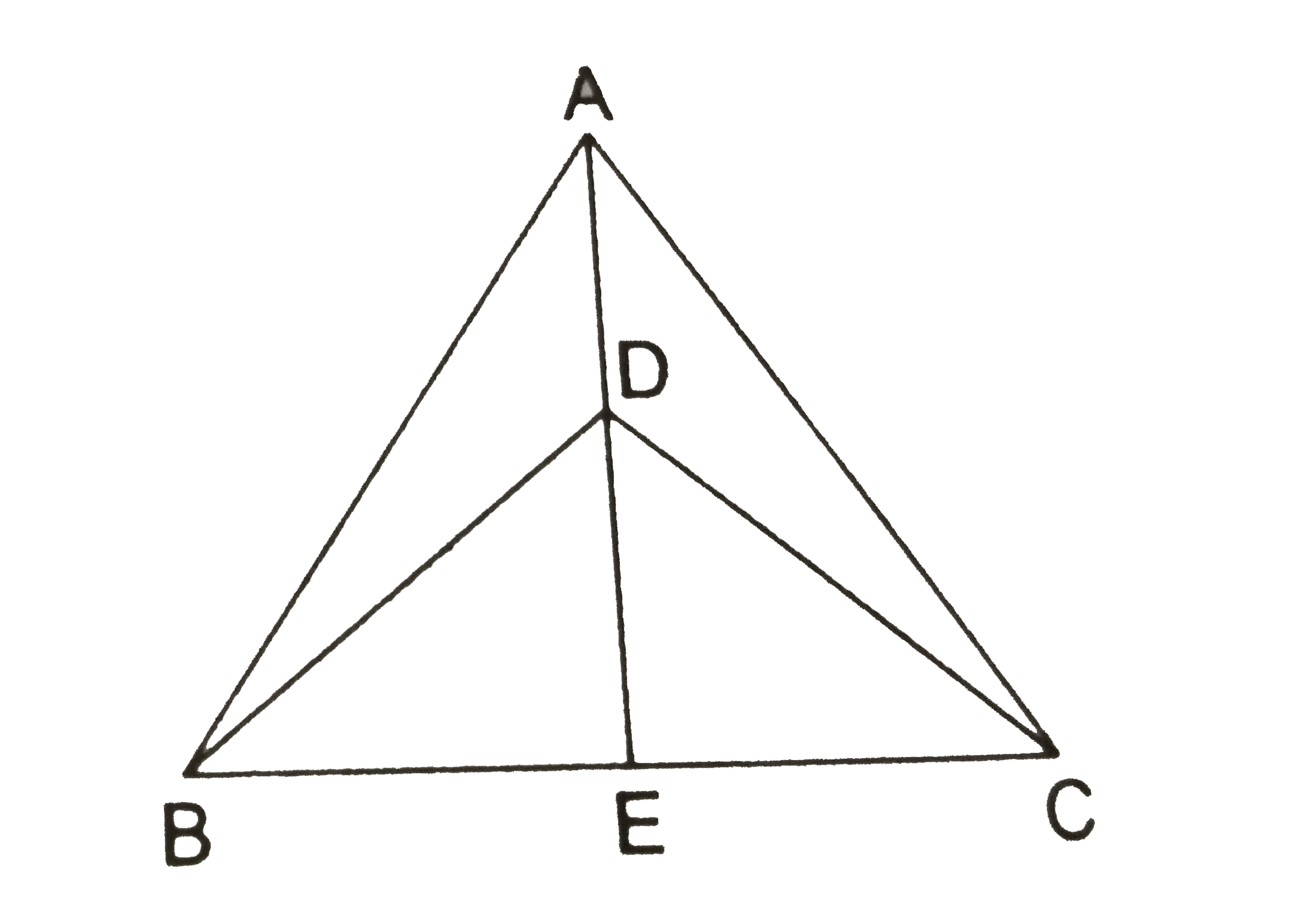
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt08:08View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.
 03:10View Solution
03:10View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए चित्र) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करें, तो दर्शाइए कि
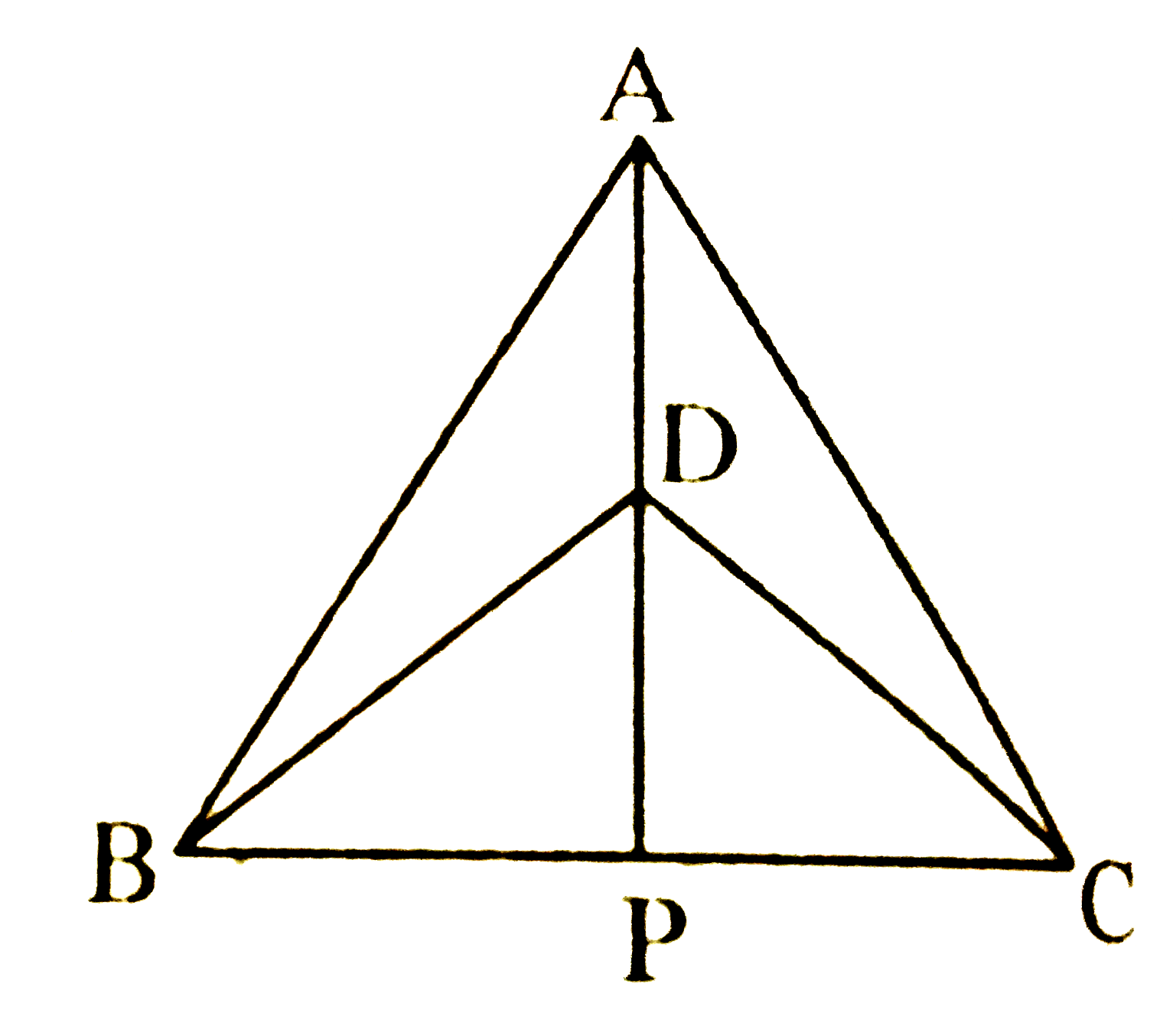
AP रेखाखंड BC का लम्ब समद्विभाजक है |02:44View Solutionत्रिभुज ABC और ΔDBCएक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकर हैं कि शीर्ष A और B भुजा BC के एक ही ओर स्थित हैं | यदि AD को बढ़ाने पर वह BC को P पर प्रतिच्छेदित सिध्द करो AP,angleA को समद्विभाजित करता है |
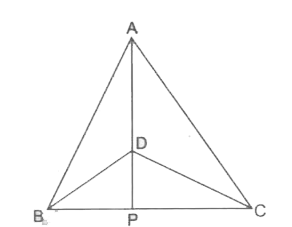
04:22View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) △ABD≅△ACD
(ii) △ABP≅△ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
 05:19View Solution
05:19View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt05:11View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
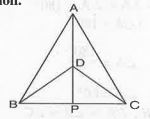 ).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.05:03View Solution
).If AD is extended to intersect BC at P, show that ΔABD≅ΔACD.05:03View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
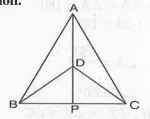 ).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.03:17View Solution
).If AD is extended to intersect BC at P, show that ΔABP≅ΔACP.03:17View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
 ).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.05:54View Solution
).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.05:54View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
 ).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.08:09View Solution
).If AD is extended to intersect BC at P, show that AP is the perpendicular bisector of BC.08:09View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.07:51View Solution

