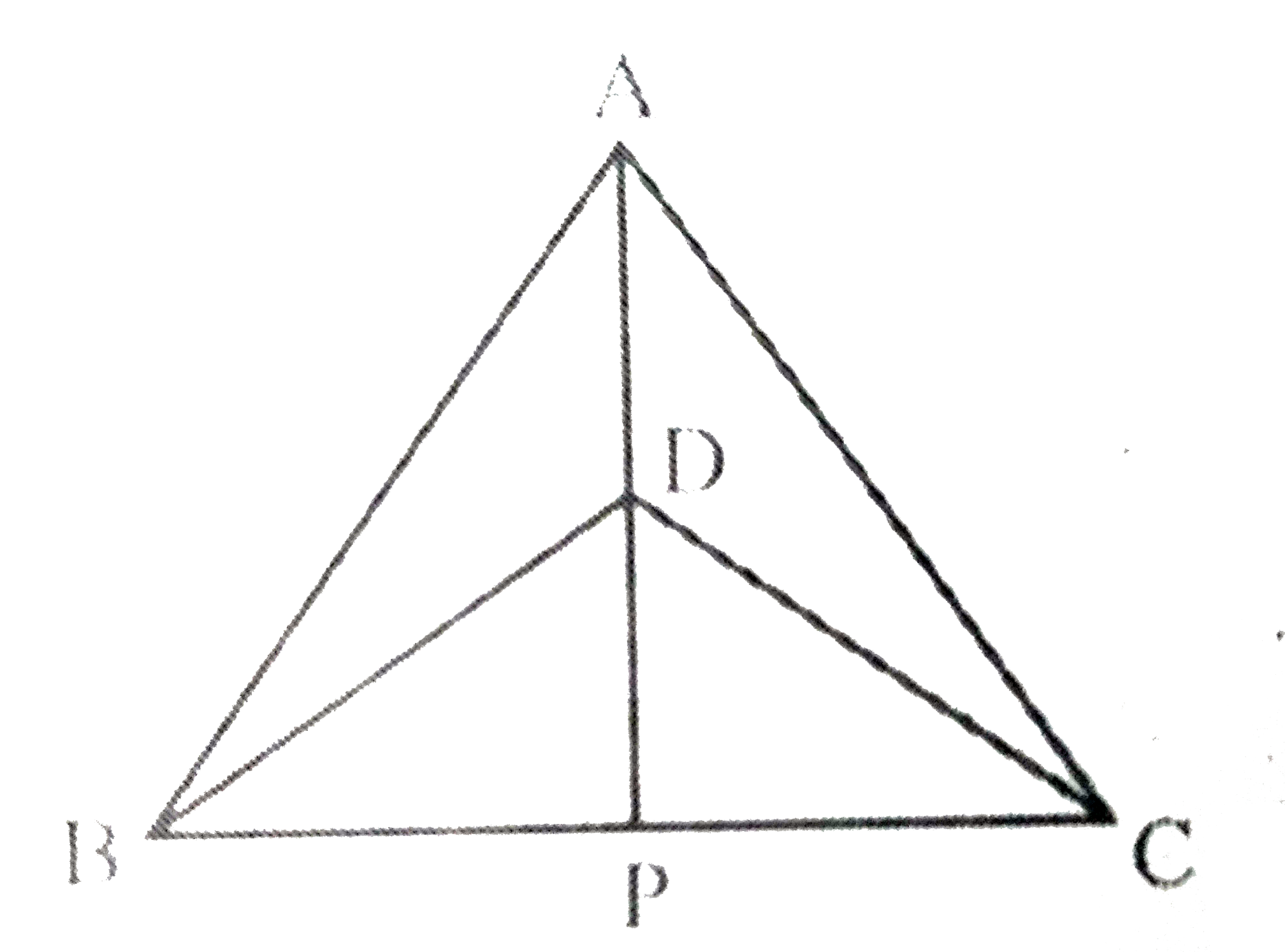
Triangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.
To prove that line segment AP bisects angles BAC and BDC, we will follow these steps:
Step 1: Draw the Diagram
Draw triangles ABC and DBC with the following properties:
- Triangle ABC is isosceles with AB = AC.
- Triangle DBC is isosceles with DB = DC.
- Extend line AD to intersect line BC at point P.
Step 2: Identify Congruent Triangles
In triangles ABD and ACD:
- We have AD = AD (common side).
- Since triangle ABC is isosceles, we know that AB = AC.
- Since triangle DBC is isosceles, we know that BD = DC.
Thus, by the Side-Side-Side (SSS) congruence criterion, we can conclude:
- Triangle ABD ≅ Triangle ACD.
Step 3: Establish Angle Relationships
From the congruence of triangles ABD and ACD, we can say:
- Angle BAD = Angle CAD (corresponding angles of congruent triangles).
Step 4: Conclude that AP Bisects Angle BAC
Since angle BAP = angle PAC (from step 3), we conclude that:
- Line segment AP bisects angle BAC.
Step 5: Analyze Triangles BDP and CDP
Now consider triangles BDP and CDP:
- We have DP = DP (common side).
- From step 4, we established that BP = PC (since BP = PC from the previous congruence).
- We also have BD = CD (since triangle DBC is isosceles).
Thus, by the SSS congruence criterion, we can conclude:
- Triangle BDP ≅ Triangle CDP.
Step 6: Establish Angle Relationships for BDC
From the congruence of triangles BDP and CDP, we can say:
- Angle BDP = Angle CDP (corresponding angles of congruent triangles).
Step 7: Conclude that AP Bisects Angle BDC
Since angle BDP = angle CDP, we conclude that:
- Line segment AP bisects angle BDC.
Final Conclusion
We have shown that line segment AP bisects both angles BAC and BDC.
---
Draw triangles ABC and DBC with the following properties:
- Triangle ABC is isosceles with AB = AC.
- Triangle DBC is isosceles with DB = DC.
- Extend line AD to intersect line BC at point P.
In triangles ABD and ACD:
- We have AD = AD (common side).
- Since triangle ABC is isosceles, we know that AB = AC.
- Since triangle DBC is isosceles, we know that BD = DC.
- Triangle ABD ≅ Triangle ACD.
From the congruence of triangles ABD and ACD, we can say:
- Angle BAD = Angle CAD (corresponding angles of congruent triangles).
Since angle BAP = angle PAC (from step 3), we conclude that:
- Line segment AP bisects angle BAC.
Now consider triangles BDP and CDP:
- We have DP = DP (common side).
- From step 4, we established that BP = PC (since BP = PC from the previous congruence).
- We also have BD = CD (since triangle DBC is isosceles).
- Triangle BDP ≅ Triangle CDP.
From the congruence of triangles BDP and CDP, we can say:
- Angle BDP = Angle CDP (corresponding angles of congruent triangles).
Since angle BDP = angle CDP, we conclude that:
- Line segment AP bisects angle BDC.
We have shown that line segment AP bisects both angles BAC and BDC.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
Triangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
ΔABP≅ΔACP
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D and AP is the perpendicular bisector of BC
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
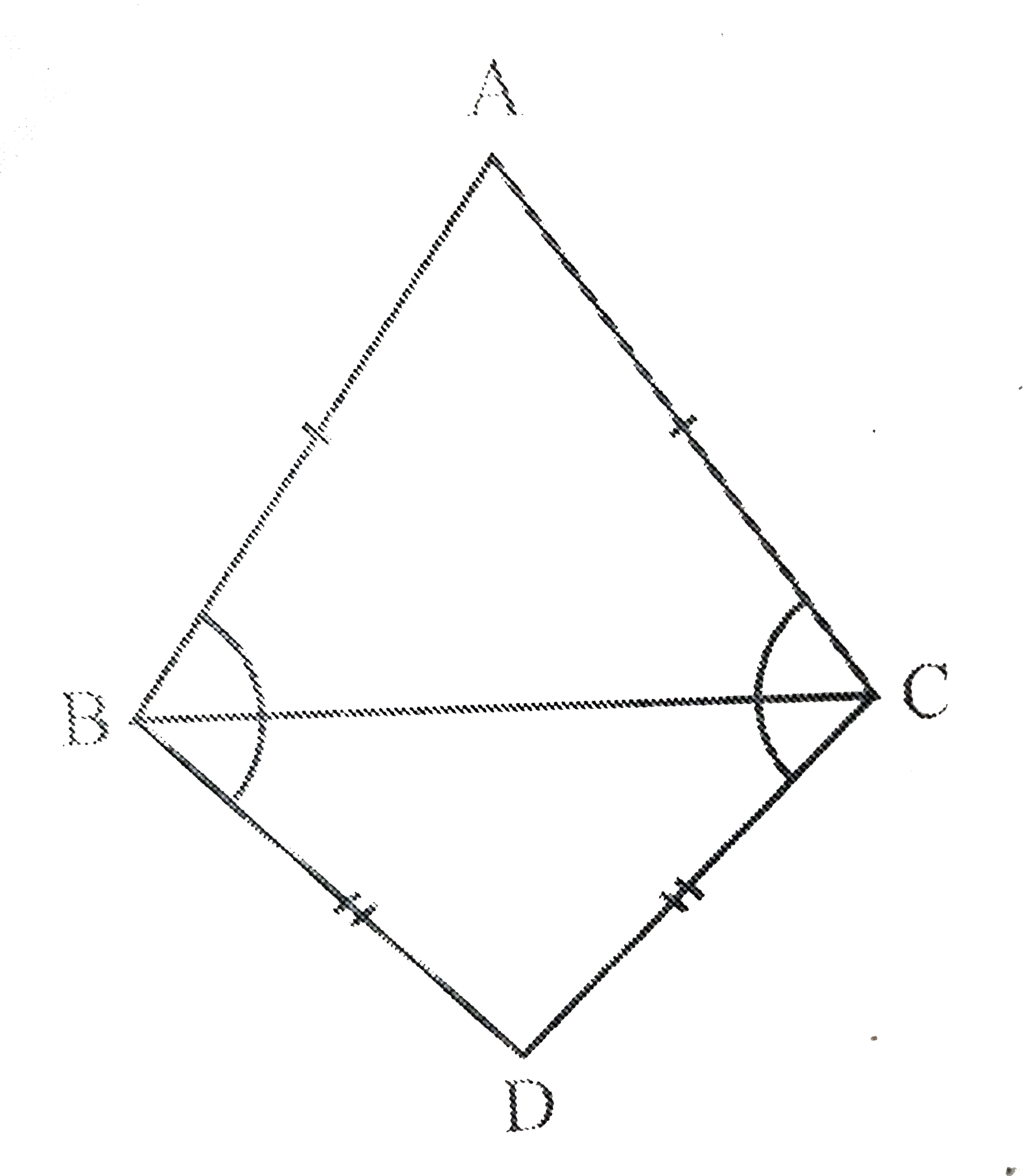
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View Solution