△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) △ABD≅△ACD
(ii) △ABP≅△ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
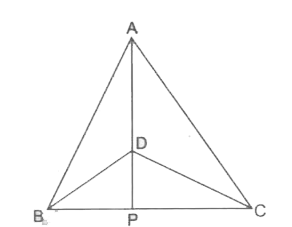 Solution in Kannada
Solution in Kannada
Step by step video & image solution for triangleABC and triangleDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that: (i) triangleABD ~= triangleACD (ii) triangleABP ~= triangleACP (iii) AP bisects angleA as well as angleD (iv) AP is the perpendicular bisector of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.4
6 Videos
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.5 (Optional)
4 Videos
- TRIANGLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLES EXERCISE - EXERCISE 5.2
8 Videos
- SURFACE AREAS AND VOLUMES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERSICE 13.8
10 Videos
Similar Questions
Show that in a right angled triangle, the hypotenuse is the longest side.
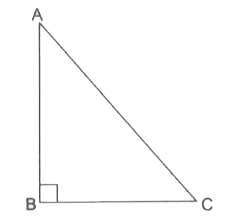
View SolutionABC is a triangle . Locate a point in the interior of △ABC which is equidistant from all the vertices of △ABC.
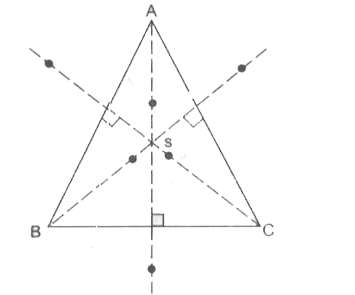
View SolutionIn an isosceles ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Joint A to O. Show that:
(ii) OB = OC
(ii) AO bisects ∠A
View SolutionFind the volume of a sphere whose radius is
(i) 7 cm,
(ii) 0.63m
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
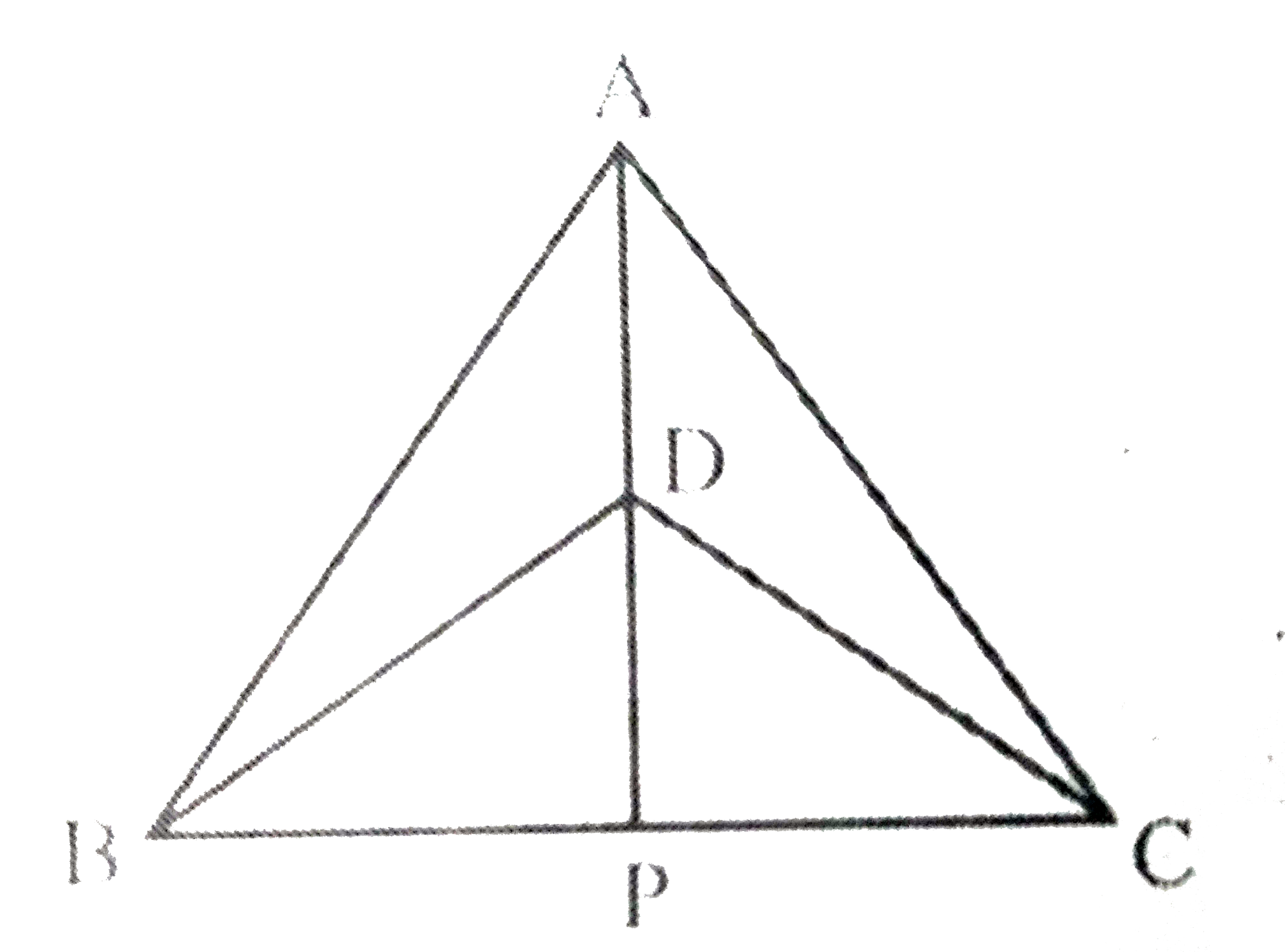
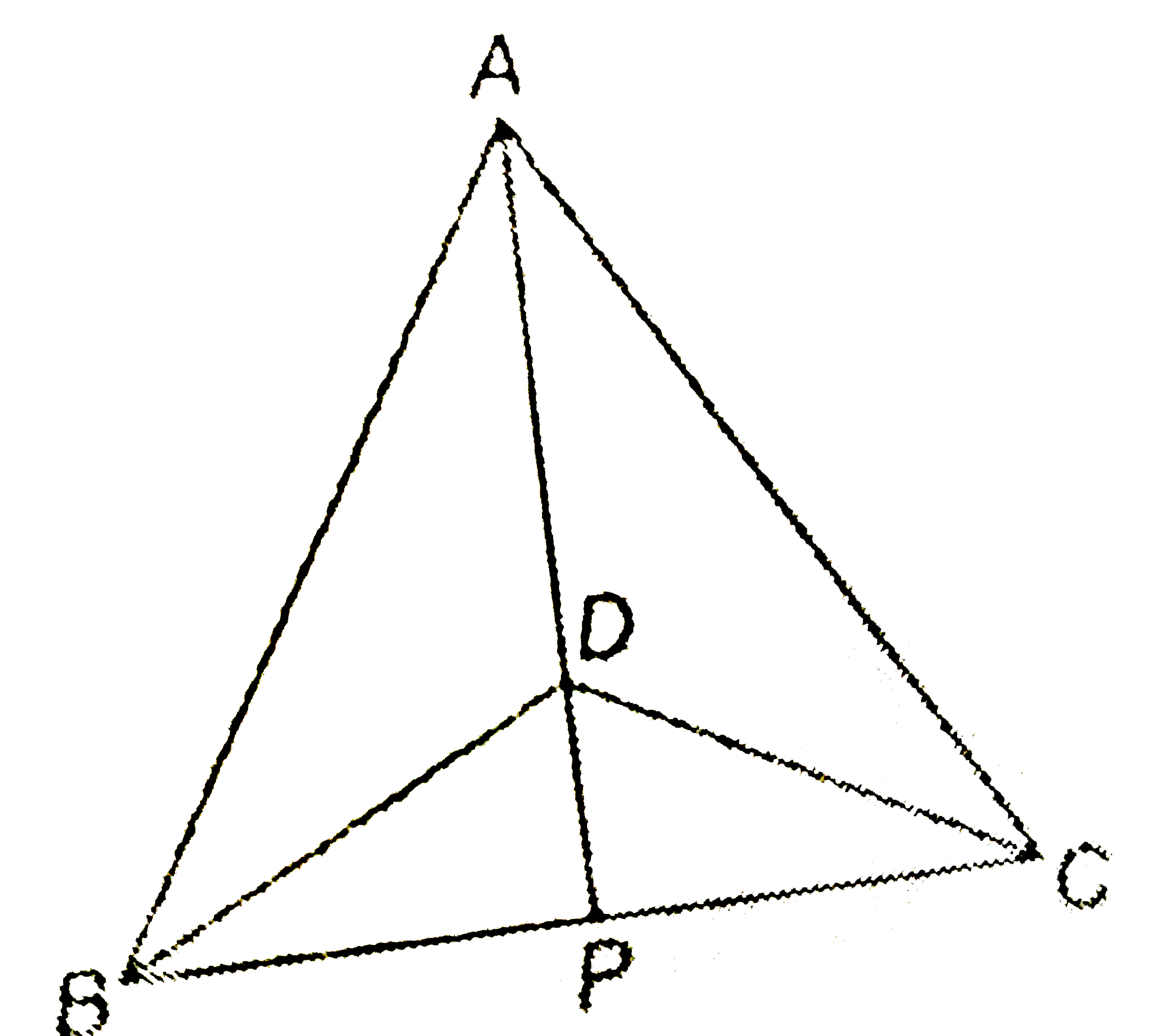
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
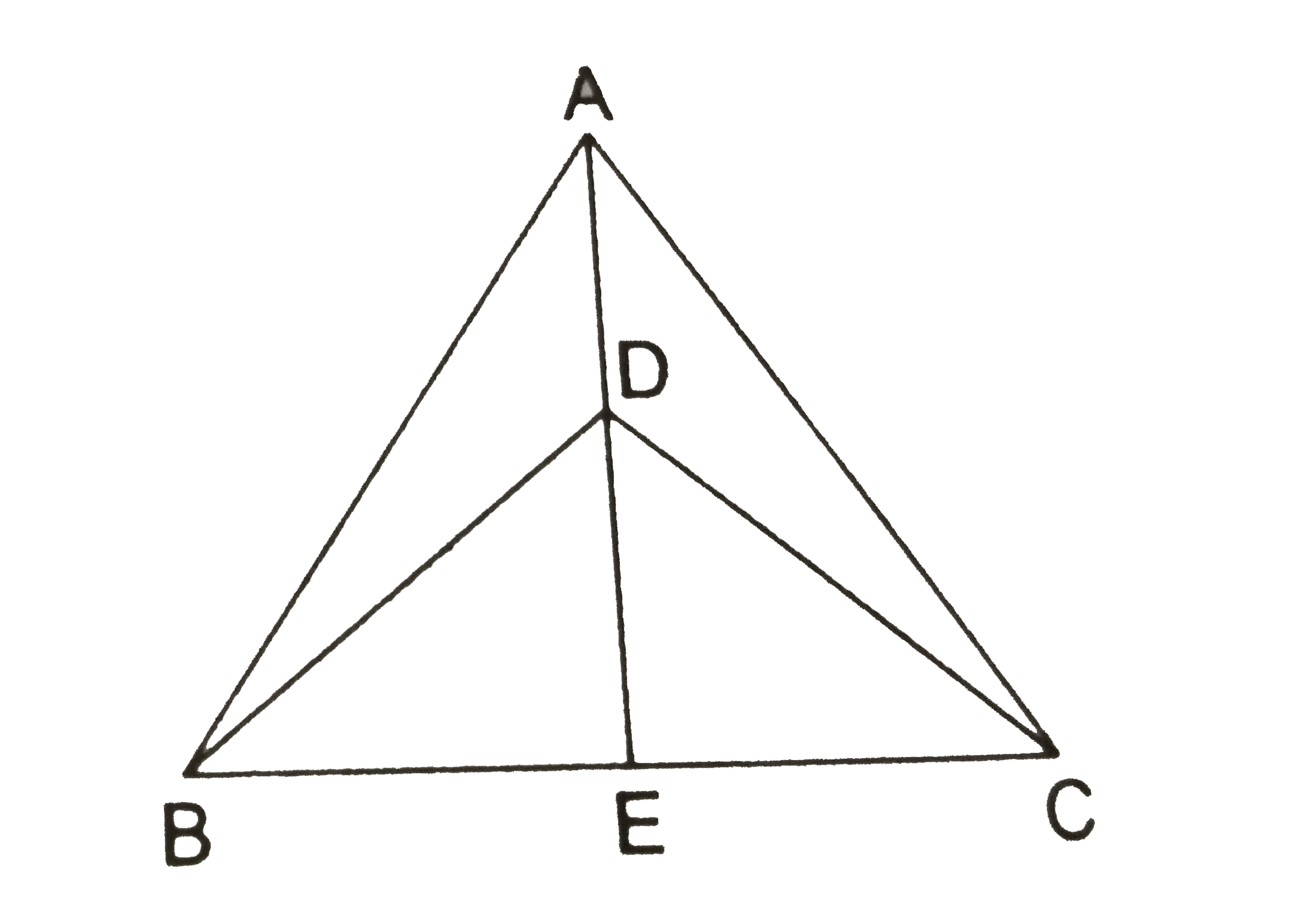
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखंड BC का लम्ब समद्विभाजक है।

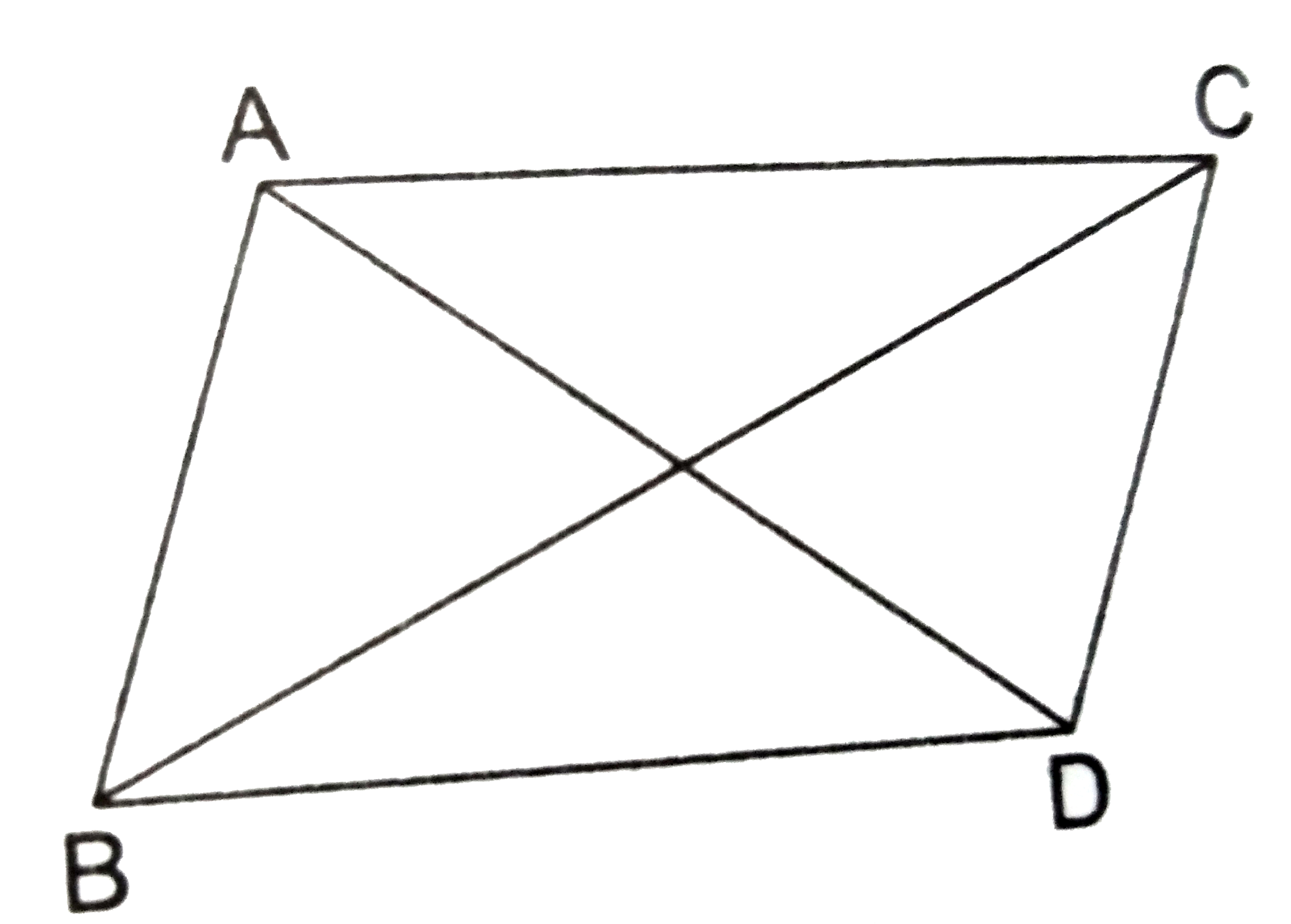
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View SolutionΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए चित्र) | यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करें, तो दर्शाइए कि
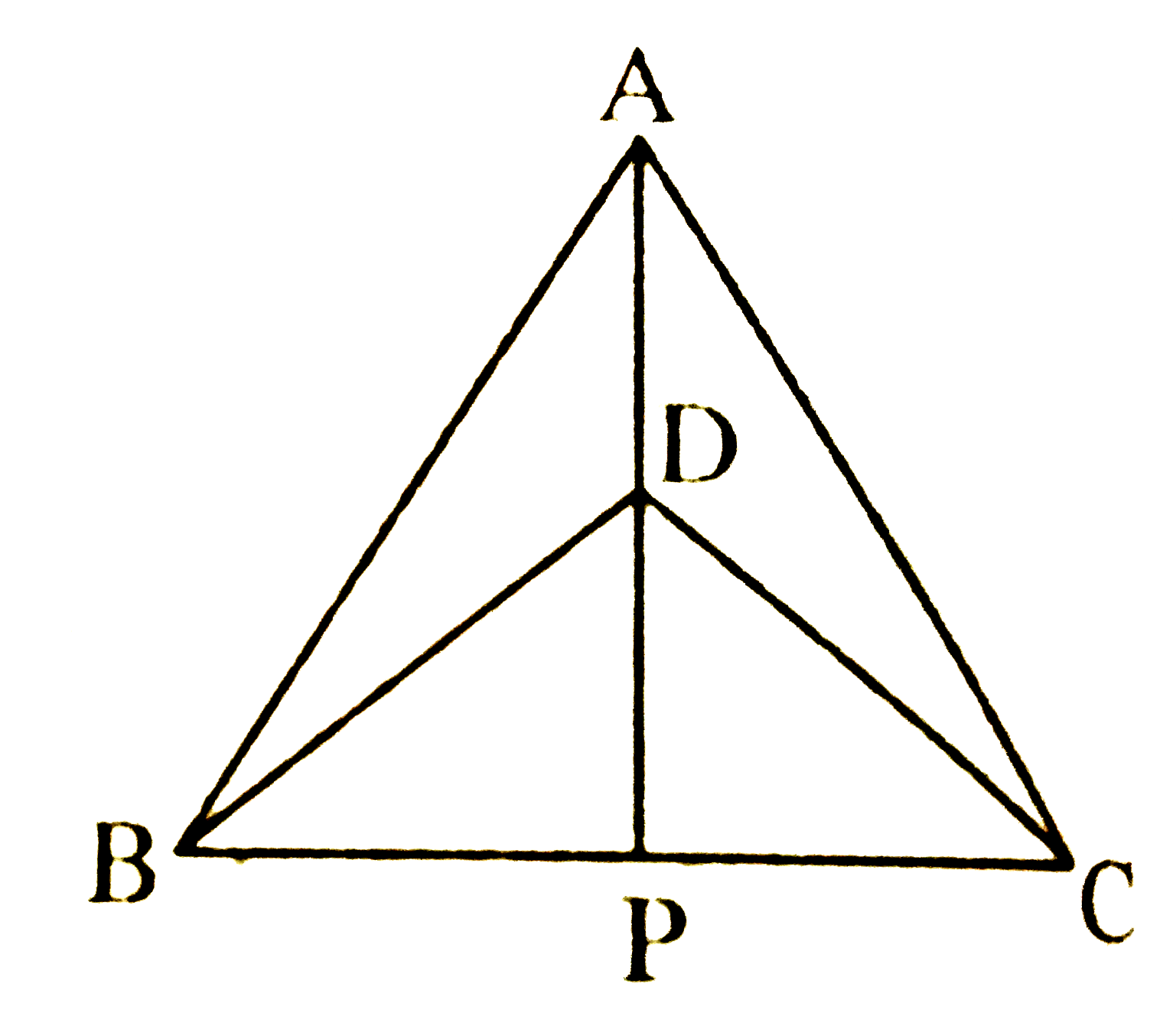
AP रेखाखंड BC का लम्ब समद्विभाजक है |
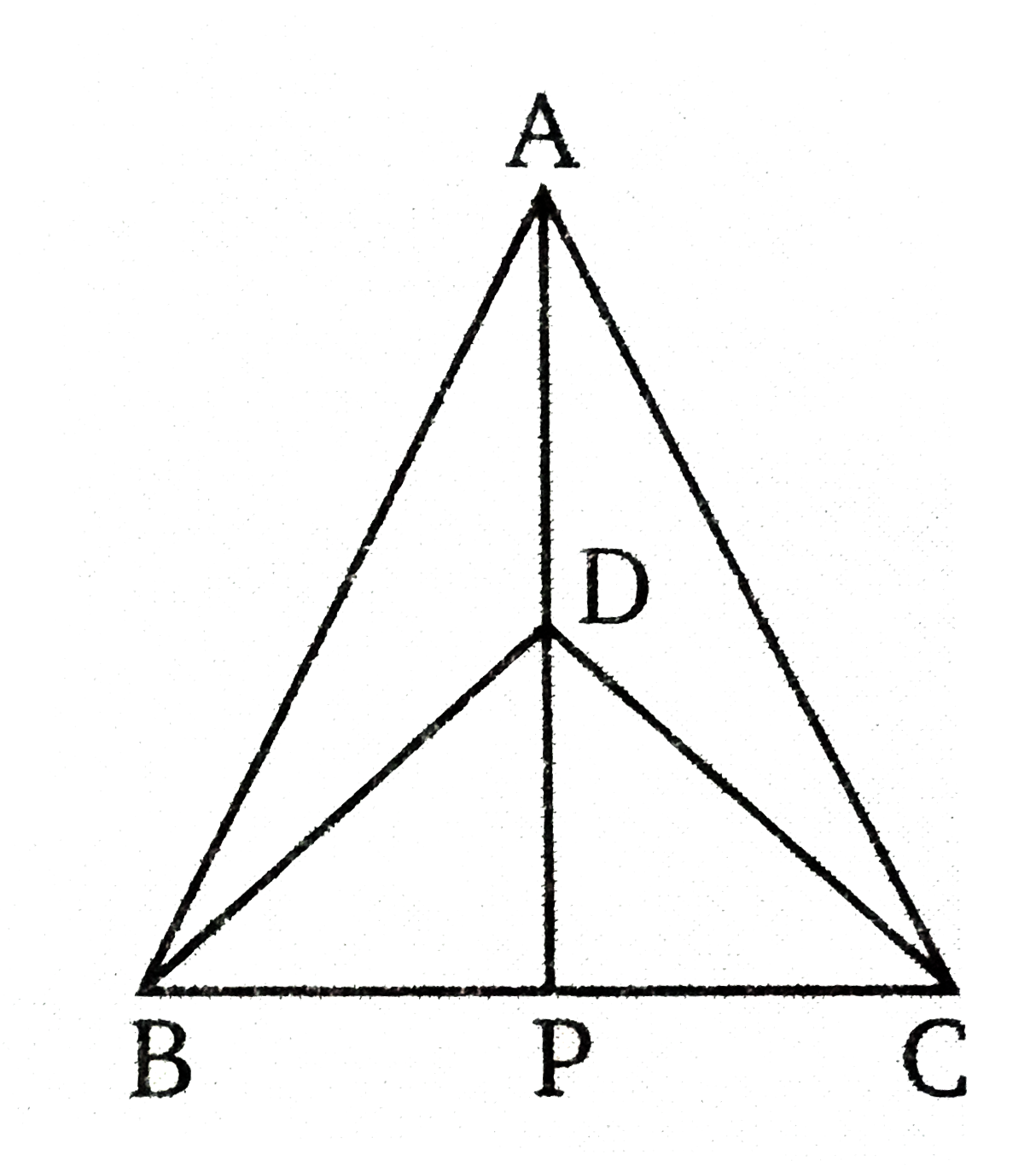
View Solutionसमान आधार BC पर दो समद्विबाहु त्रिभुज ABC तथा DBC है तथा BC की समान भुजा पर शीर्ष A और Dहै यदि AD को बढ़ाने पर ,BC को P पर प्रतिच्छेद करती है ।
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP,∠A व ∠Dको समद्विभाजित करते है ।
(iv) AP, BC का लम्बर्द्धक है ।
View Solutionत्रिभुज ABC और ΔDBCएक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकर हैं कि शीर्ष A और B भुजा BC के एक ही ओर स्थित हैं | यदि AD को बढ़ाने पर वह BC को P पर प्रतिच्छेदित सिध्द करो AP,angleA को समद्विभाजित करता है |
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View Solution△ ABC and △ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that, ( i ) △ABD=△ACD(ii)△ABP=△ACP (iii) AP bisects ∠ A as well as ∠ D. (iv) AP is the perpendicular bisector of BC
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (See Fig.
 ).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.
).If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D.
View Solution
