Question

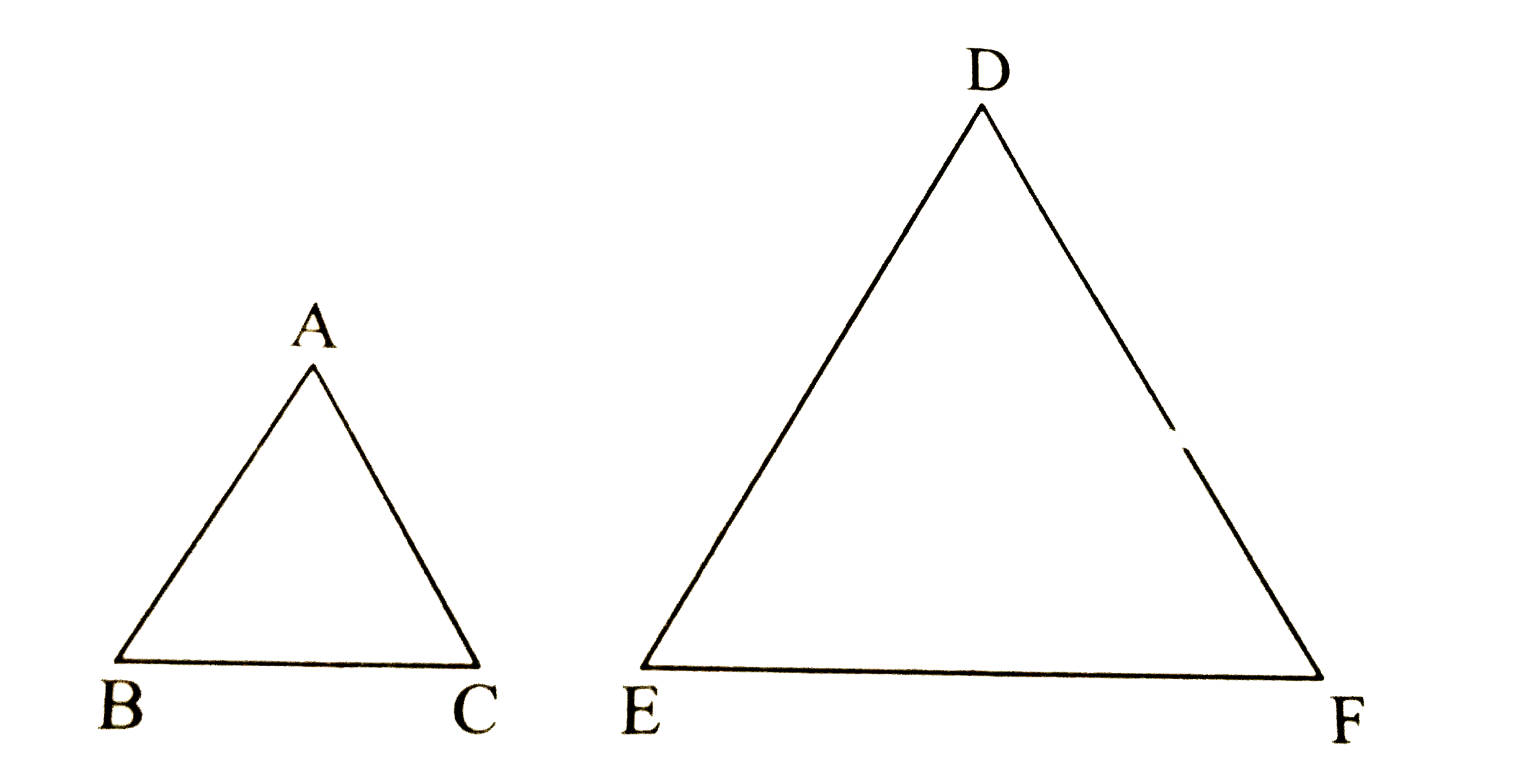
$\Delta ABC$ and $\Delta DEF$ are equilateral triangles. If $A(\Delta ABC):A(\Delta DEF)=1:2$ and $AB=4$, find DE.

Explanation

`DeltaABC` and `DeltaDEF` are equilateral triangles.
`:./_A=/_B=/_C=/_D=/_E=/_F=60^(@)`
….(Angles of equilateral triangle)
In `DeltaABC` and `DeltaDEF`
`{:(/_A~=/_D),(/_B~=/_E):}}`……Each measures `60^(@)`
`:.DeltaABC~DeltaDEf`……..(AA test of similarity)
By the theorem of areas of similar triangles,
`(A(DeltaABC))/(A(DeltaDEF))=(AB^(2))/(DE^(2))`..........1
`A(DeltaABC):A(DeltaDEF)=1:2` and `AB=4`
......(Given)..2
`:.1/2=(4^(2))/(DE^(2))`..(From 1 and 2 ]
`:.DE^(2)=4^(2)xx2`
`:.DE=4sqrt(2)`
.....(Taking square roots of both the sides)
`DE=4sqrt(2)`.