ΔABC is an equilateral triangle. Point D is on seg BC such that BD=15AC. Prove : that 25AD2=21AB2
The correct Answer is:25AD2=21AB2
Topper's Solved these Questions
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - UNIQUE PRACTICE SESSION MCQ.S (1 MARKS QUESTION )11videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - UNIQUE PRACTICE SESSION MCQ.S (2 MARKS QUESTION )12videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PROBLEM SET 230videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 523videos
PROBABILITY
- BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT6videos
QUADRATIC EQUATIONS
Similar Questions
ΔABC is an equilateral triangle. Point D is on side BC such that BD=15BC then prove 25AD2=21AB2.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionThe perimeters of two similar triangles are 25cm and 15cm respectively. If one side of the first triangle is 9cm, find the length of the corresponding side of the second triangle.
OR
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD2=7AB2View SolutionABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn ΔABC,
seg AD⊥ seg BC,
DB=3CD.
Prove that 2AB2=2AC2+BC2.
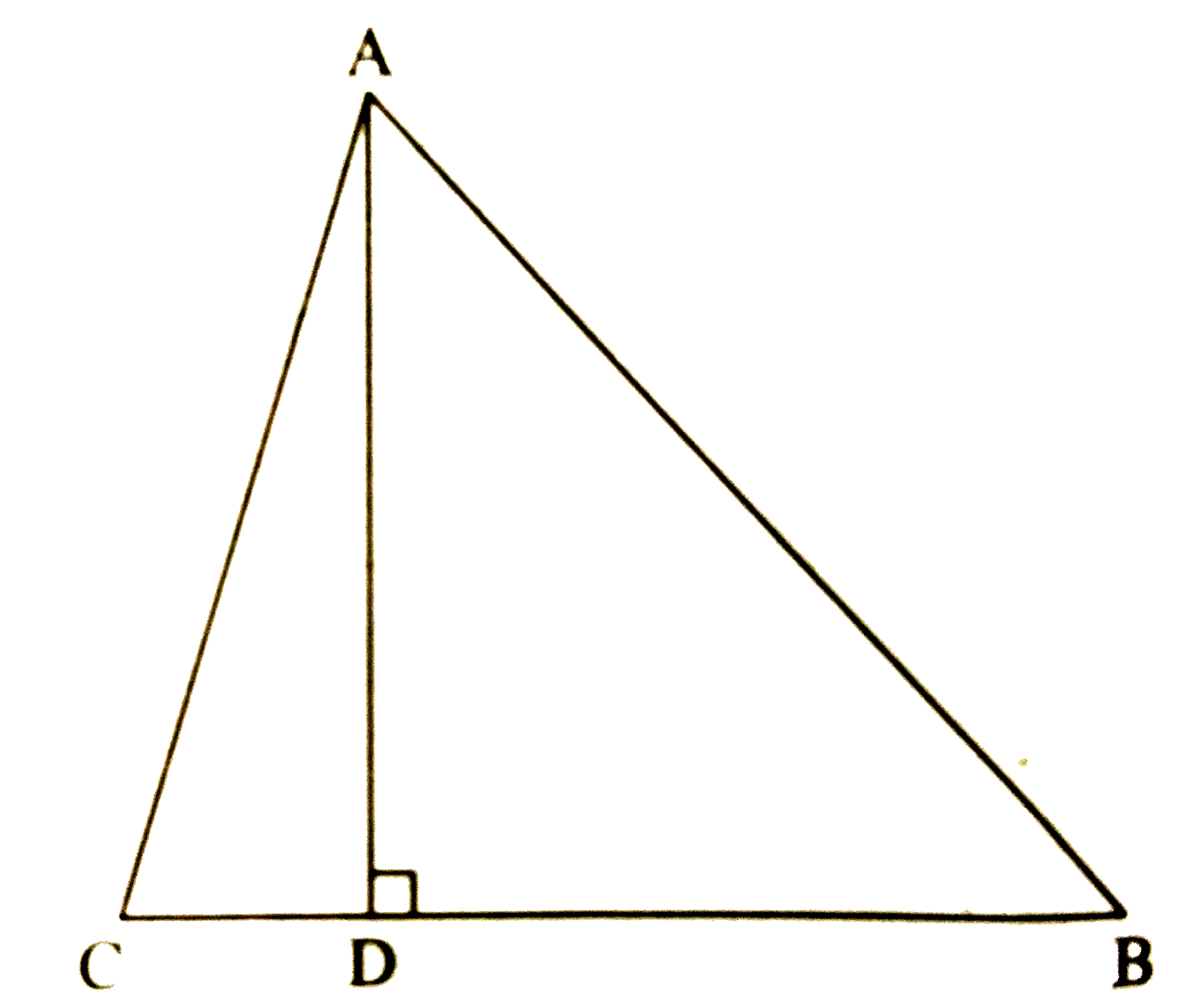 View Solution
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
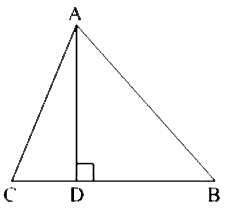 View Solution
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn ΔABC seg AD⊥segBC,DB=3CD Prove that 2AB2=2AC2+BC2
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CDView Solution

