Diagonals AC and BD of a trapezium ABCD with ABCD intersect each where at O. Prove that ar (AOD)=ar(BOC).
Step by step video & image solution for Diagonals A C and B D of a trapezium A B C D with A B C D intersect each where at Odot Prove that ar ( A O D)=a r( B O C)dot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-D5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PRACTICE TEST2videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(AOD)=ar(BOC) . Prove that ABCD is a trapezium.
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
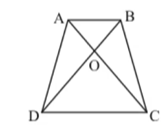 View Solution
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
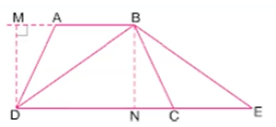 View Solution
View Solution

