Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
(i) A∩B, (ii) A∪B, (iii) B-A
To solve the problem, we will follow these steps to draw a Venn diagram and shade the required regions:
1. Draw the Universal Set:
- Start by drawing a rectangle to represent the universal set (let's label it as U).
2. Draw the Two Sets:
- Inside the rectangle, draw two overlapping circles. Label one circle as Set A and the other as Set B. Ensure that the circles overlap to show the relationship between the two sets.
3. Identify the Regions:
- The overlapping area of the two circles represents the intersection of Set A and Set B, denoted as A∩B.
- The entire area covered by both circles represents the union of Set A and Set B, denoted as A∪B.
- The part of Set B that does not overlap with Set A represents the difference of Set B and Set A, denoted as B−A.
4. Shade the Regions:
- (i) Shade A∩B: Shade the overlapping region of the two circles. This shaded area represents the intersection of Set A and Set B.
- (ii) Shade A∪B: Shade the entire area of both circles (including the overlapping region). This shaded area represents the union of Set A and Set B.
- (iii) Shade B−A: Shade the part of Set B that is outside of Set A. This shaded area represents the elements that are in Set B but not in Set A.
Final Diagram:
- You will have a rectangle representing the universal set, two overlapping circles for sets A and B, and the specified regions shaded accordingly.
- Start by drawing a rectangle to represent the universal set (let's label it as U).
- Inside the rectangle, draw two overlapping circles. Label one circle as Set A and the other as Set B. Ensure that the circles overlap to show the relationship between the two sets.
- The overlapping area of the two circles represents the intersection of Set A and Set B, denoted as A∩B.
- The entire area covered by both circles represents the union of Set A and Set B, denoted as A∪B.
- The part of Set B that does not overlap with Set A represents the difference of Set B and Set A, denoted as B−A.
- (i) Shade A∩B: Shade the overlapping region of the two circles. This shaded area represents the intersection of Set A and Set B.
- (ii) Shade A∪B: Shade the entire area of both circles (including the overlapping region). This shaded area represents the union of Set A and Set B.
- (iii) Shade B−A: Shade the part of Set B that is outside of Set A. This shaded area represents the elements that are in Set B but not in Set A.
- You will have a rectangle representing the universal set, two overlapping circles for sets A and B, and the specified regions shaded accordingly.
Topper's Solved these Questions
Similar Questions
Two sets A and B are such that A∩B=π. Draw a Venn-diagram to show the relationship between A and B. Shade the region representing :
(i) A∪B, (ii) (A∪B)', (iii) B-A, (iv) B∩A'
View SolutionDraw a Venn-diagram to show the relationship between sets A and B , such that A⊆B. Now shade the region representing :
(i) A∪B, (ii) B'∩A, (iii) A∩B, (iv) (A∪B)'
View SolutionFor two overlapping sets A and B, draw Venn-diagrams to represent the set
View SolutionDraw the venn diagram to represent
(i) A∩(B−A)'<br>(ii)A∪B(B∩A)'
View SolutionIf A and B are two sets such that A⊆B, then find
(i) A∪B
(ii) A∩B.
View SolutionProve (A∩B)'=(A'∪B')
View SolutionThe adjoining diagram shows a relation between the set A and B. Write this relation
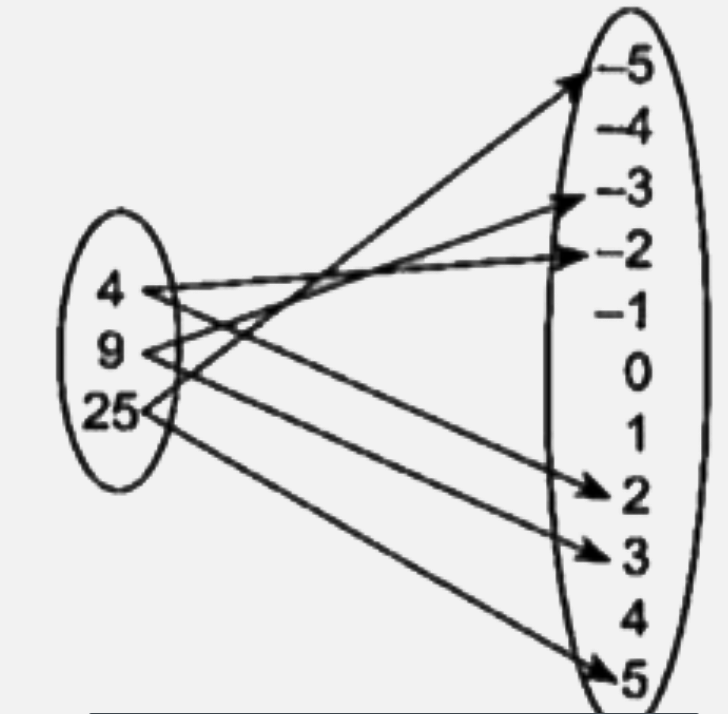
(i) In roster form
(ii) In set builder form
View SolutionFrom the given diagram find:
(i) A∪B
(ii) A'∩B
(iii) A-B
(iv) B-A
(v) (A∪B)'

View SolutionFor any two sets A and B, prove that :
(i) (A∩B)∪(A−B)=A
(ii) A∪(B−A)=A∪B.
View SolutionIf A =factors of 24} and B={factors of 36}, find, (i) A∩B, (ii) A∪B
View Solution
