Prove (A∩B)'=(A'∪B')
To prove the set identity (A∩B)′=(A′∪B′), we will demonstrate that both sides of the equation represent the same set.
1. Start with the Left-Hand Side (LHS):
We begin with the left-hand side of the equation:
LHS=(A∩B)′
This denotes the complement of the intersection of sets A and B.
2. Understanding the Complement:
By the definition of the complement, if X is an element of (A∩B)′, it means that X is not an element of A∩B:
X∉(A∩B)
3. Using the Definition of Intersection:
The statement X∉(A∩B) implies that X does not belong to both A and B simultaneously. Therefore, we can express this as:
X∉A or X∉B
4. Expressing in Terms of Complements:
The above statement can be rewritten using the complements of sets A and B:
X∈A′ or X∈B′
This means that X belongs to either the complement of A or the complement of B.
5. Using Union:
From the previous step, we can conclude that:
X∈A′∪B′
Thus, we have shown that:
(A∩B)′⊆(A′∪B′)
6. Now, Proving the Right-Hand Side (RHS):
Next, we will show that:
(A′∪B′)′⊆(A∩B)
Let Y be an element of (A′∪B′)′. This means:
Y∉(A′∪B′)
7. Understanding the Union's Complement:
The statement Y∉(A′∪B′) implies that:
Y∈A and Y∈B
This is because if Y is not in the union, it must be in both sets A and B.
8. Conclusion:
Hence, we can conclude:
Y∈A∩B
Therefore, we have shown that:
(A′∪B)′⊆(A∩B)
9. Combining Both Results:
Since we have shown both:
(A∩B)′⊆(A′∪B′)and(A′∪B)′⊆(A∩B)
We can conclude that:
(A∩B)′=(A′∪B′)
Final Result:
Thus, we have proved that:
(A∩B)′=(A′∪B′)
We begin with the left-hand side of the equation:
LHS=(A∩B)′
This denotes the complement of the intersection of sets A and B.
By the definition of the complement, if X is an element of (A∩B)′, it means that X is not an element of A∩B:
X∉(A∩B)
The statement X∉(A∩B) implies that X does not belong to both A and B simultaneously. Therefore, we can express this as:
X∉A or X∉B
The above statement can be rewritten using the complements of sets A and B:
X∈A′ or X∈B′
This means that X belongs to either the complement of A or the complement of B.
From the previous step, we can conclude that:
X∈A′∪B′
Thus, we have shown that:
(A∩B)′⊆(A′∪B′)
Next, we will show that:
(A′∪B′)′⊆(A∩B)
Let Y be an element of (A′∪B′)′. This means:
Y∉(A′∪B′)
The statement Y∉(A′∪B′) implies that:
Y∈A and Y∈B
This is because if Y is not in the union, it must be in both sets A and B.
Hence, we can conclude:
Y∈A∩B
Therefore, we have shown that:
(A′∪B)′⊆(A∩B)
Since we have shown both:
(A∩B)′⊆(A′∪B′)and(A′∪B)′⊆(A∩B)
We can conclude that:
(A∩B)′=(A′∪B′)
Thus, we have proved that:
(A∩B)′=(A′∪B′)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))41videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-B(Objective Type Question(One option is correct))13videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - EXAMPLE24videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers11videos
SEQUENCES AND SERIES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason15videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If P(A∩B)=13,P(A∪B)=56andP(A)=12, then which one of the following is correct ?
AA and B are independent eventsBA and B are mutually exclusiveCmutually exclusiveDnone of these
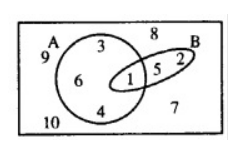
From the given diagram, find:
(i) A', (ii) B', (iii) A'∪B', (iv) (A∩B)'
Is A'∪B'=(A∩B)' ?
 View Solution
View Solutionif A and B are two sets, then prove that, (A∪B)'∪(A'∩B)=A'.
View SolutionIf P(A∩B)=1/3,P(A∪B)=5/6 and P(A)=1/2, then which one of the following is correct ?
View SolutionProve the distributive law and De Morgan's law.
(i) A∩(B∪C)=(A∩B)∪(A∩C)
(ii) (A∪B)'=A'∩B'View SolutionIf A and B are stes, then A∩(A∪B)=
View SolutionLet A, B and C be three events such that P(C )=0
Statement-1: P(A∩B∩C)=0
Statement-2: P(A∪B∪C)=P(A∪B)View SolutionDraw the venn diagram to represent
(i) A∩(B−A)'<br>(ii)A∪B(B∩A)'View Solution

