Draw the graph of f(x)=[√x],x∈[0,16), where [⋅] denotes the greatest ineger function.
Video Solution
Text Solution
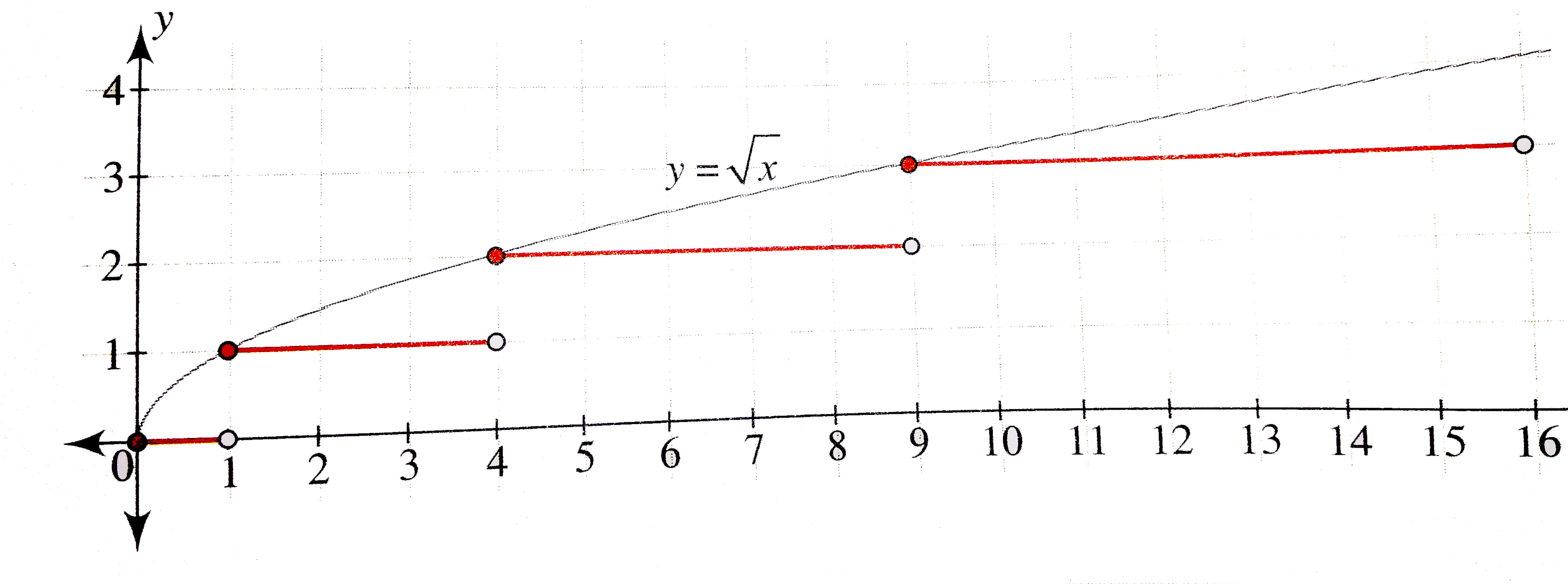
f(x)=[√x],x∈[0,16)
y=√x is a monotonically increasing function in x∈[0,16).
So f(x)=[√x] willl be discontinuous when √x is an integer.
For x∈[0,16),√x∈[0,4).
So [√x] is discontinuous when √x=1,2,3orx=1,4,9.
Hence f(x)=[√x]=⎧⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪⎩0,x∈[0,1)or√x∈[0,1)1,x∈[1,4)or√x∈[1,2)2,x∈[4,9)or√x∈[2,3)3,x∈[9,16)or√x∈[3,4)
The graph of the function is as shown in the following figure.
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
If f(x)=[x]−[x4],x∈R where [x] denotes the greatest integer function, then
Alimx→4+f(x) exists but limx→4−f(x) does not existBf is continuous at x=4CBoth limx→4−f(x)andlimx→4+f(x) exist but are not equalDlimx→4−f(x) exists but limx→4+f(x) does not existIf f(x)=[x]|x|,x≠0, where [.] denotes the greatest integer function, then f'(1) is
A−1B1Cnon-existentDnone of these
Draw the graph of y=[sinx],x∈[0,2π], where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=[cosx],x∈[0,2π], where [⋅] represents the greatest integer function.
View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionIf f(x)=[2x], where [.] denotes the greatest integer function, then
View SolutionDraw the graph of y=[x]+√x−[x], where[⋅] denotes the greatest ineger function.
View Solution
