Draw the graph of f(x)=|x−1|+|2x−3|. Find the range of the function.
Video Solution
Text Solution
Here f(x)=|x−1|+|2x−3|
=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩1−x+3−2x,x<1x−1+3−2x,1≤x≤32x−1+2x−3,x>32
=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩4−3x,x<12−x,1≤x≤323x−4,x>32
Quick method :
Function changes definition at x−1=0and2x−3=0orx=1andx=3/2. Since the graph of the function is a straight line in each of the regions (−∞,1),(1,3/2)and(3/2,∞), we need to check the values at some particular values of x to draw the graphs in each region.
f(1)=1
f(3/2)=0.5
f(0)=4
f(2)=1+1=2
Thus, we plot the points A(0,4),B(1,1),C(3/2,1/2)andD(2,2).
Plotting these points and connecting with straight line, we have the following graph.
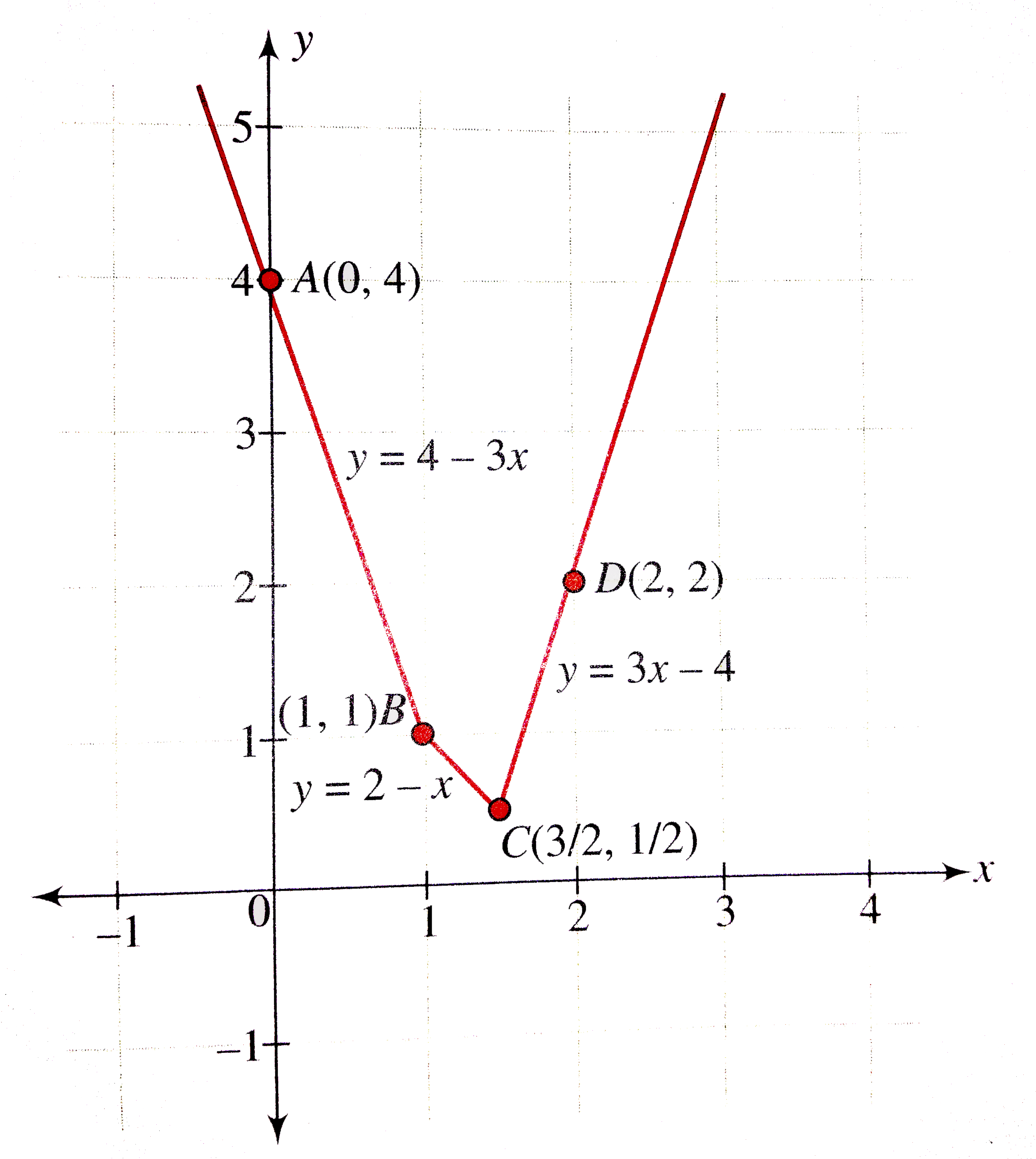
From the graph, the range of the function is [0.5,∞).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the sum is 240 and average is 40, find the number of quantities.
A5B2C3D6
Draw the graph of f(x)=x2−3
View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|.
View SolutionFind the range of the function, f(x)=x|x|
View SolutionDraw the graph of f(x)=loge(√1−x2).Find the range of the function .Also find the values of k if (x) has two distinct real roots.
View SolutionDraw the graph of:
y=f(x)=3sin(2x−1).View SolutionDraw the graph of the function f(x)=2x−|x|
View SolutionFind the range of function f(x)=1+3cos2x
View Solution

