Draw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.Solution in Bengali
We have y=f(x)=3x4−4x3=x3(3x−4)
The sign scheme of y=f(x) is as follows.
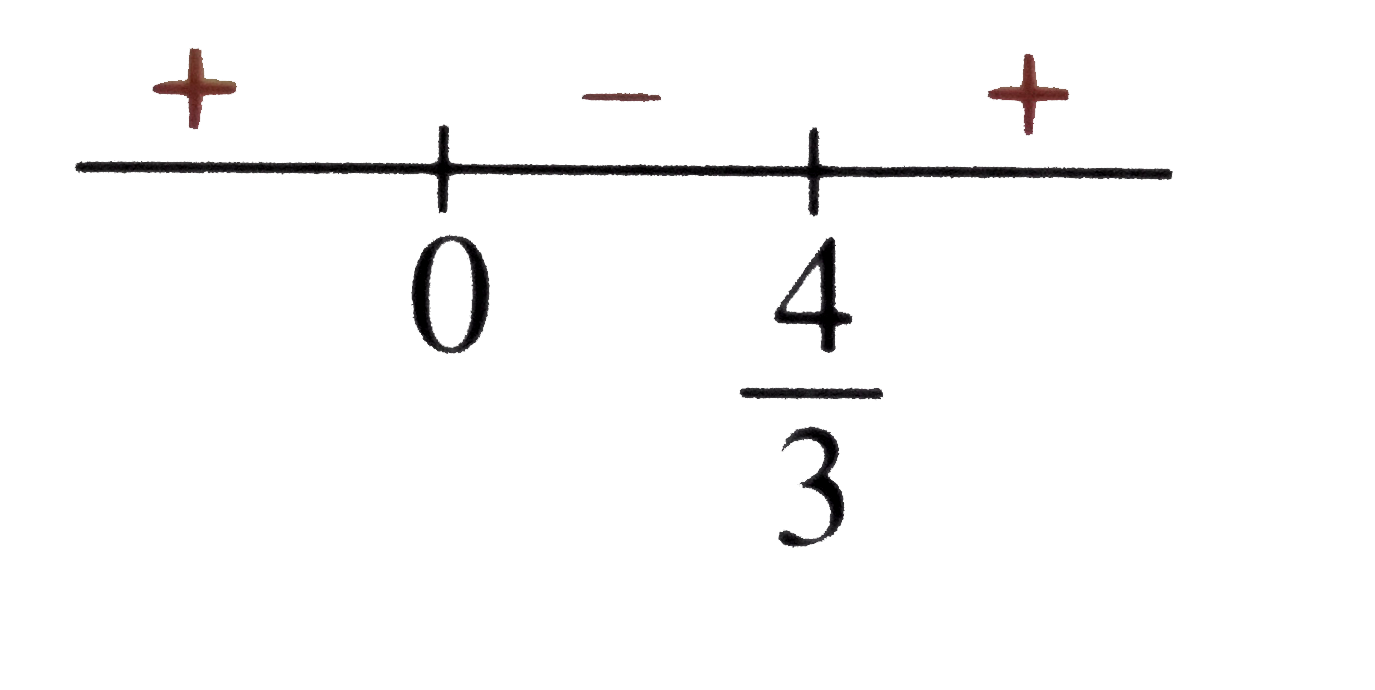
(3x−4)→ Graph crosses the x-axis at x=4/3 without touching the x-axis.
x2→ Graph crosses the x-axis at (0,0) and also touches the x-axis at this point.
f'(x)=12x3−12x2
=12x2(x−1)
f'(x)=0
∴ x=0,1
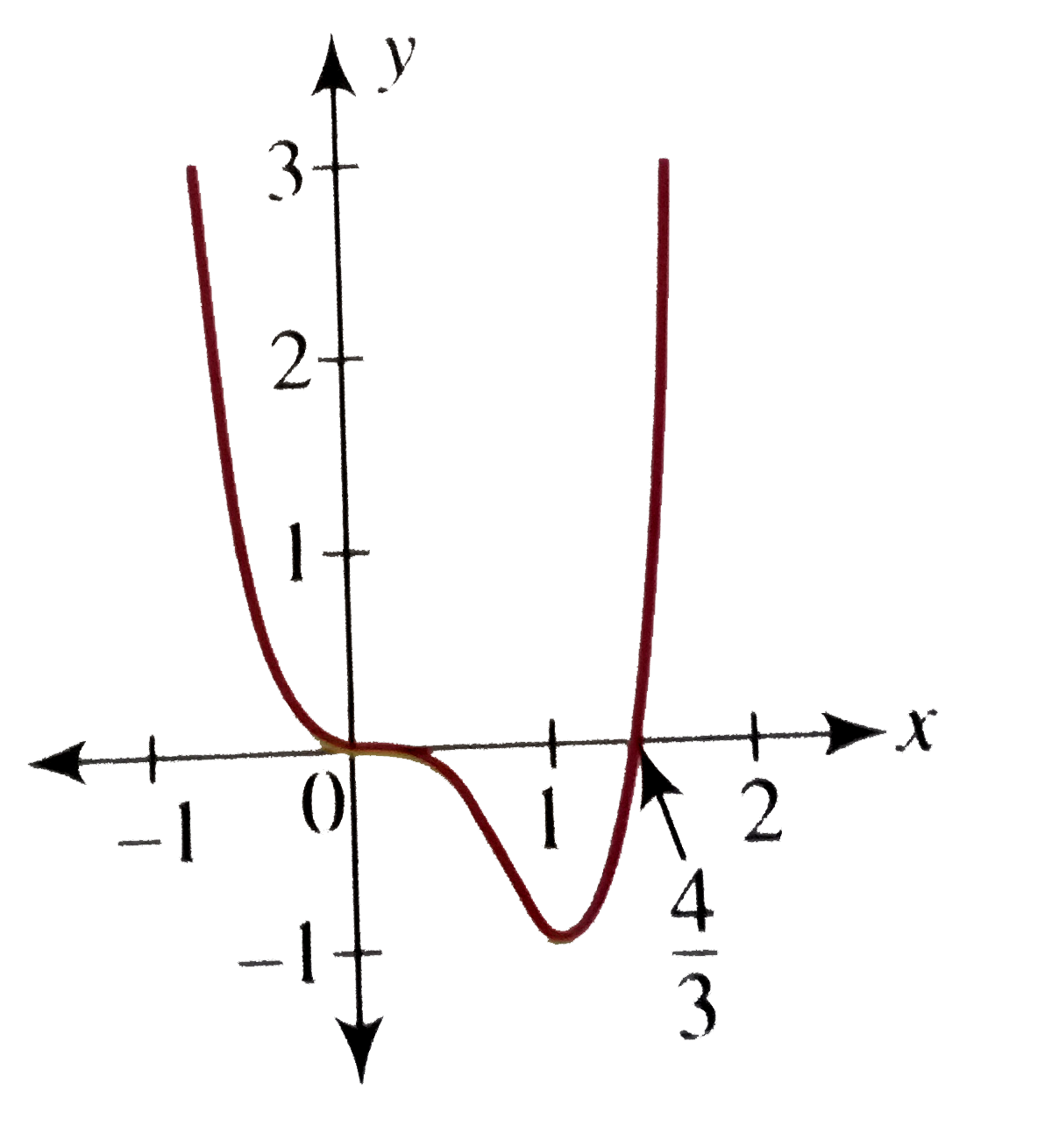
f'(x)<0,if x<1, where f(x) decreases
f'(x)>0,if x>1, where f(x) increases
x=1 is the point of minima.
Also f''(x)=36x2−24x=12x(3x−2)
f''(x)=0,if x=0,2/3, which are points of inflection .
The graph of the function is as shown in the following figure.
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION
78 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
View SolutionDraw the graph of y=1(1/x).
View SolutionDraw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=2x3+3x2−12x
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=xx−5
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=ex1−ex
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=x33−logx
View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=sinxcosx+5,x∈(0,2π)
View SolutionFor the function f(x)=4x3+3x2−6x+1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.
View SolutionDraw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.
View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=3x4−8x3+6x2+12
View SolutionTheory OF Monotonicity || Local Extremum Points
View SolutionIllustration Based upon Monotonicity || Illustration Based upon Local Extremum Points
View Solution
