Draw the graph of y=xex. Find the range of the function. Also find the point of inflection.Solution in Bengali
We have y=f(x)=xex
Clearly, the domain of the function is R.
f(0)=−0
and f(x)=0 when x=0
f′(x)=ex+xex=ex(1+x)
f′(x)>0 for x<−1, where f(x) increases
f′(x)<0 for x<−1, where f(x) decreases
f′(x)=0∴x=−1
Also at x=−1,dydx, Changes sign from negative to positive, hence x=−1 is the point of minima,
f(−1)=−e−1=−1/e
When x→∞,f(x)→∞
Also limx→−∞xex=xx→−∞e−x=1x→−∞−e−x=0
So x-axis is an asymptote.
Thus, in (−∞,−1),f(x) decreases from 0+→−1/e
In (1,∞),f(x) increases, intersecting the x-axis at x=0
f''(x)=ex(2+x)
f''(x)=0∴x=−2
So x=−2 is the point of inflection.
From the above discussion, the graph of the function is as follows:
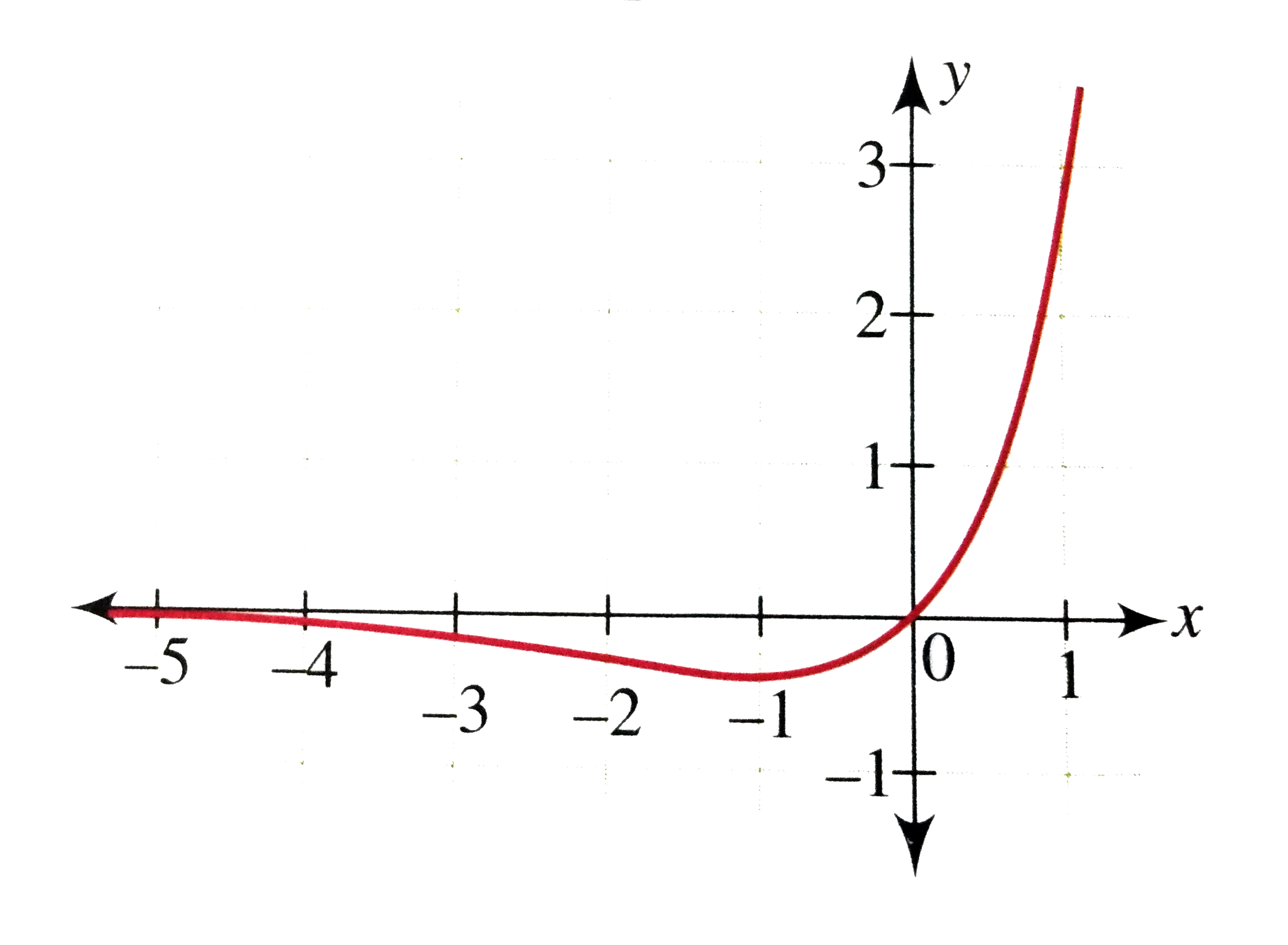
Range of the function is [f(−1),∞) or [−e−1,∞).
Topper's Solved these Questions
Similar Questions
Find the derivative of y=sin2x−cosx
02:19View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet f be a non-negative function defined on the interval [0,1]. If ∫x0√1−(f′(t))2dt=∫x0f(t)dt,0≤x≤1,and f(0)=0, then
03:01View SolutionFind the points of local maxima or minima and corresponding local maximum and minimum values of f(x)=x ex . Also, find the points of inflection, if any:
03:24View SolutionDraw the graph of y=sin−1(logex). Also find the point of inflection.
06:31View SolutionDraw the graph of y=xex. Find the range of the function. Also find the point of inflection.
06:27View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
08:32View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
07:15View SolutionDraw the graph of y=xex.Also
(i) Find the range of the functionf
(ii) Find the point of inflection.
(iii)Find the values of k if 1xex=k has two distinct real roots03:03View SolutionDraw the graph of y=sin−1(logex). Also find the point of inflection.
07:08View SolutionDraw the graph of y=xex. Find the range of the function. Also find the point of inflection.
04:28View SolutionDraw the graph of f(x)=ex1+ex. Also find the point of inflection.
04:17View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
05:55View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
03:46View SolutionDraw the graphs of y=x and y=−x in the same graph. Also, find the coordinates of the point where the two lines intersect.
04:43View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x1+x203:37View Solution

