E and F are respectively the midpoints of the non-parallel sides AD and BC of a trapezium ABCD. Prove that
(i) EF∣∣AB,
(ii) EF=12(AB+CD).
GIVEN A trapezium ABCD in which E and F are midpoints of sides AD and BC respectively .
TO PROVE (i) EF||AB, (ii) EF=12(AB+CD).
CONTRUCTION Join DF and produce it to meet AB produced in P.
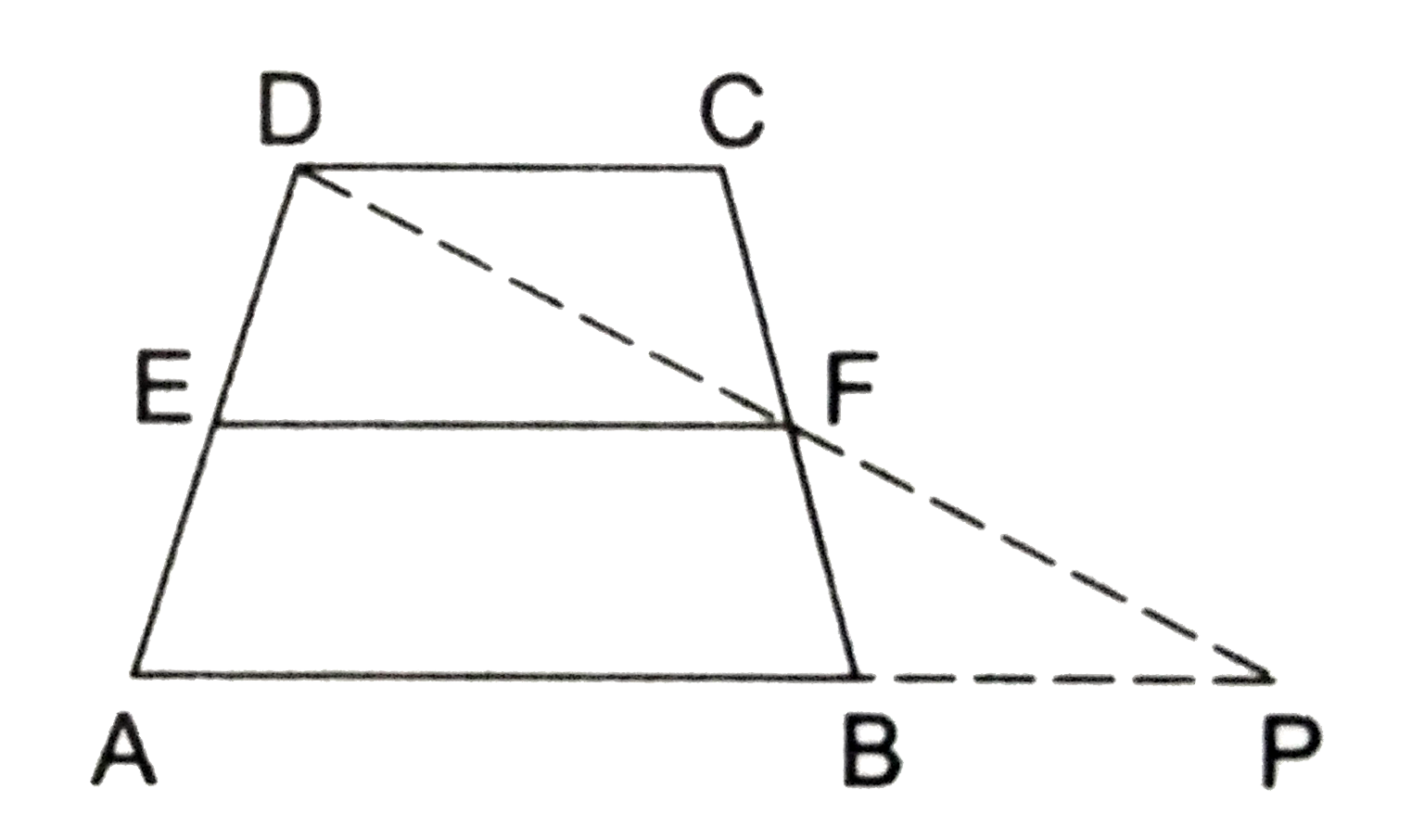
PROOF In △DCF and PBF we have
∠DFC=∠PFB (vert . opposite ∠)
CF=BF (∵ F is the midpoint of BC)
∠DCF=∠PBF (alt. interior ∠)
∴△DCF≅△PBF (ASA-criterion).
And so, DF=PFandCD=BP (c.p.c.t.).
Now, in △DAP, we have
E is the midpoint of AD and F is the midpoint of DP. [∵DF=PF]
∴ EF||AP and EF=12AP [by midpoint theorem]
⇒ EF||AB and EF=12(AB+BP).
Hence, EF||AB and EF=12(AB+CD).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXAMPLE
32 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
The line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View Solution
Knowledge Check
If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD10/3, 9 and 12 cmIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD103, 9 and 12 cmA line EF is drawn parallel to the parallel sides AB and CD of a trapezium ABCD where E lies on AD and F lies on BC. If AE:ED=2:1 then what is BF : BC ?
AA)2:3BB)3:2CC)2:1DD)1:2
ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionThe parallel sides AB and CD of a trapezium ABCD are 9 cm and 3 cm respectively. The non-parallel sides AD and BC are 4 cm and 6 cm respectively. A line EF parallel to AB divides the trapezium ABCD into two trapeziums of equal perimeter. Find the ratio in which each of the non-parallel sides is divided in
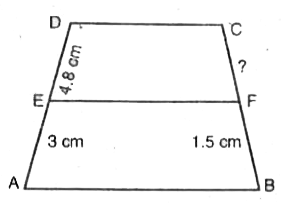
View SolutionABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
View Solution
