Evaluate the area bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$ above the x-axis.

Video Solution

Text Solution

Verified by Experts

The given ellispse meets the x-axis at A (-2,0) and B (2,0)
$\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 y = \frac{3}{2} . \sqrt{4 - x^{2}}$
$∴$ required area $= 2 \int - 2 y d x = \frac{3}{2} . 2 \int - 2 \sqrt{4 - x^{2}} d x$
$= 2 \times \frac{3}{2} \times 2 \int 0 \sqrt{4 - x^{2}} d x$
$= 6 . π / 2 \int 0 {cos}^{2} θ d θ$ where x=2 sin $θ$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

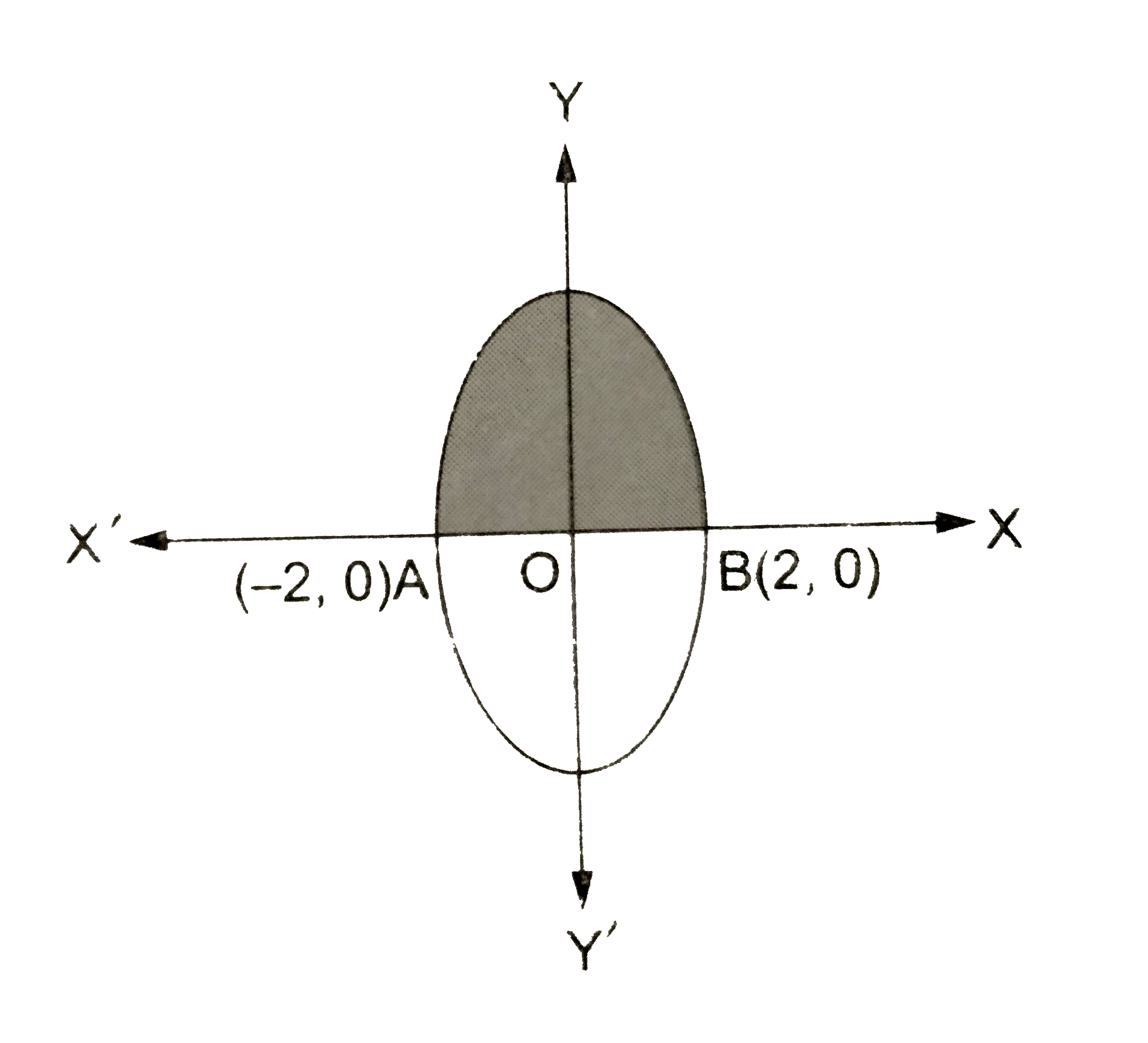
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Area bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1$ is equal to
A $6 π$ sq units
B $3 π$ sq units
C $12 π$ sq units
Darea bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$
Question 2 - Select One
The area bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{25} = 1$ is
A $2 π s q . u n i t s$
B $5 π s q . u n i t s$
C $20 π s q . u n i t s$
D $10 π s q . u n i t s$
Question 3 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq unit
B $\frac{3 π}{2}$ sq unit
C $\frac{9 π}{4}$ sq unit
D $\frac{4 π}{7}$ sq unit

RS AGGARWAL-AREA OF BOUNDED REGIONS -Exercise 17

Home
Ask Doubt
Profile