Figure shows rectangle ABCD. Points A and D are on the parabola y=2x2−8, and points B and C are on the parabola y=9−x2. If point B has coordinates (−1.50,6.75), what is the area of rectangle ABCD ?
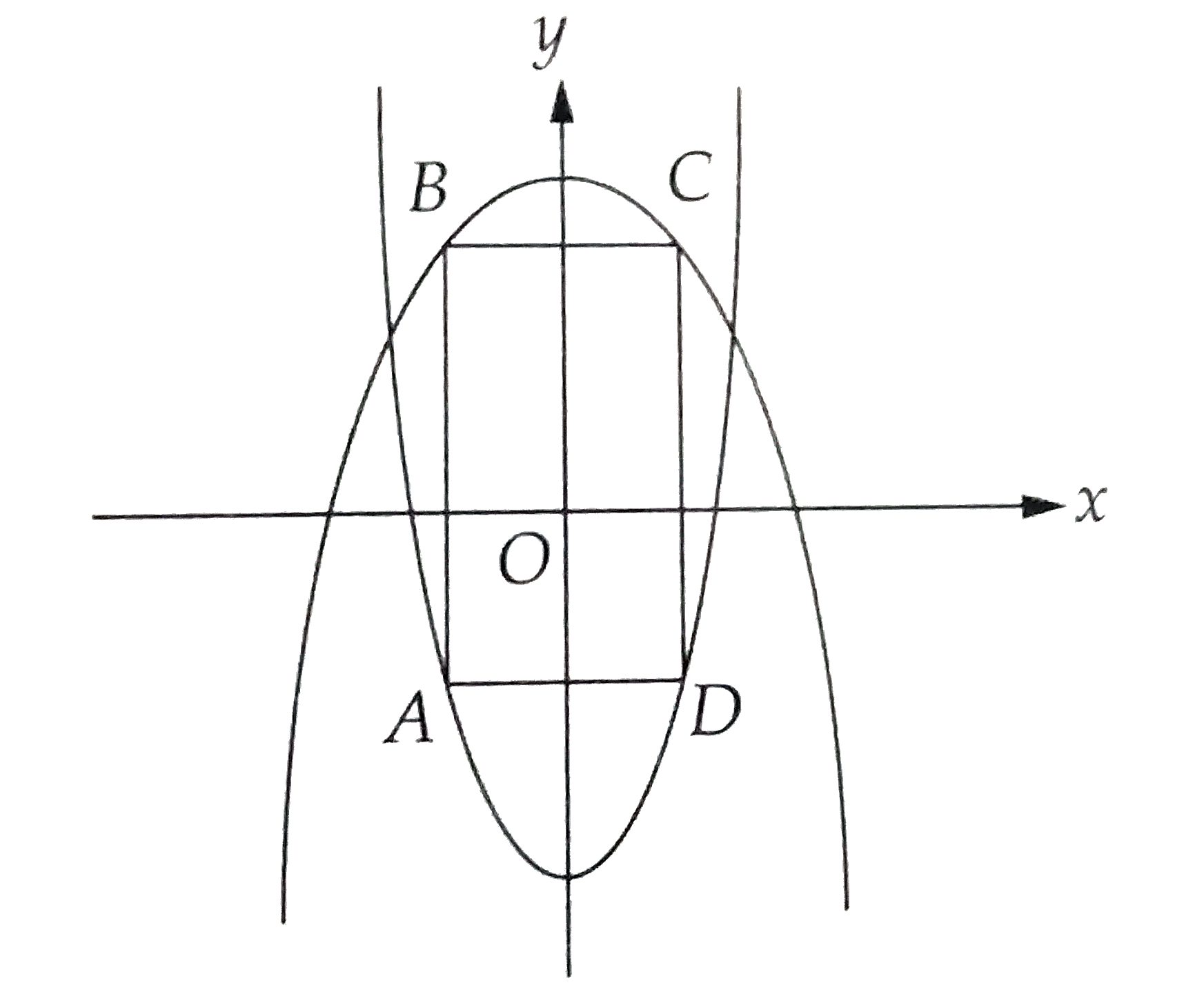
A
12.50
B
17.50
C
22.75
D
30.75
Video Solution
Text Solution
The correct Answer is:D
To find the area of the rectangle, you need the base and height. Both parabolas are symmetric with respect to the y - axis, so if the x - coordinate of point B is - 1.50, the length of segment BC, which is the base of the rectangle, is twice 1.50, or 3. To find the height of the rectangle, use the y - coordinate of point B and find the y - coordinate of point A. That's the value of y when you plug x=−1.50 into the equation y=2x2−8 :
y=2(−1.50)2−8=−3.5
So the height of the rectangle is 6.75−(−3.5)=6.7+3.5=10.25, and the area of the rectangle is 3×10.25=30.75.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
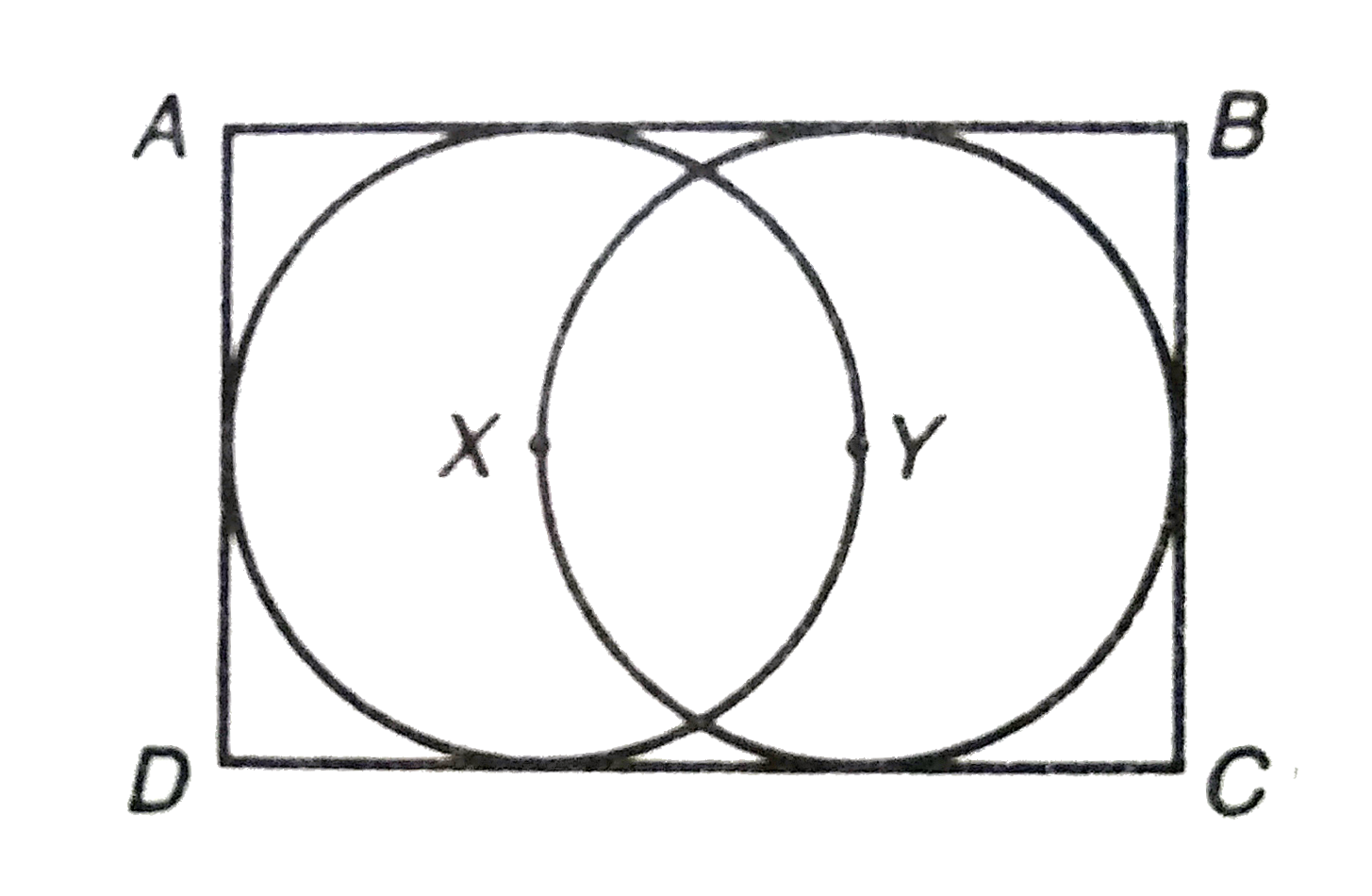
In the figure above, X and Y are the centers of two overlapping circles. If the area of each circle is 7, what is the area of rectangle ABCD?A14−17πB7+14πC28πD42π
The line x+y=6 is normal to the parabola y2=8x at the point.
View SolutionIf points A and B lie on x-axis and points C and D lie on the curve y=x2−1 below the x-axis then maximum area of rectangle ABCD is
View SolutionThe point on the parabola y2=8x whose distance from the focus is 8 has x coordinate as
View SolutionThe focal distance of the point (4,2) on the parabola x2=8y is
View SolutionThe focal distance of the point (9,6) on the parabola y2=4x is
View SolutionThe focal distance of the point (9,6) on the parabola y2=4x is
View SolutionFour points A,B,C,D lie in that order on the parabola y=ax2+bx+c. The co-ordinates of A,BandD are known as A(−2,3);B(−1,1)andD(2,7). The co-ordinates of C for which the area of the quadrilateral ABCD is greatest is
View Solution

