Find a unit vector perpendicular to each of the vector $\to a + \to b$ and $\to a - \to b$ , where $\to a = 3 ˆ i + 2 ˆ j + 2 ˆ k$ and $\to b = ˆ i + 2 ˆ j - 2 ˆ k$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\pm (\frac{2}{3} ˆ i - \frac{2}{3} ˆ j - \frac{1}{3} ˆ k)$

Answer

Step by step video, text & image solution for Find a unit vector perpendicular to each of the vector vec a+ vec b and vec a - vec b, where vec a = 3 hat i + 2 hat j + 2 hat k and vec b = hati + 2 hat j - 2 hat k. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.1
2videos
VECTOR ALGEBRA
BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.2
13videos
VECTOR ALGEBRA
BOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.3
18videos
VECTOR ALGEBRA
BOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
134videos
TRIGONOMETRIC FUNCTIONS

Similar Questions

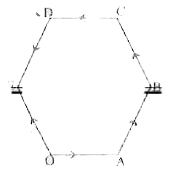
In the figure which vectors are
(i) equal (ii) collinear (iii) coinitial

05:40
View Solution
Compute the magnitude of the following vectors and identify the unit vector.
$\to a = 2 ˆ i - 3 ˆ j + 5 ˆ k$
03:20
View Solution
Find the angle between two vectors $\to a$ and $\to b$ with magnitudes $\sqrt{3}$ and 2, respectivey having $\to a . \to b = \sqrt{6}$ .
01:59
View Solution
If $A + B + C = 90^{\circ}$ then
$\frac{cot A + cot B + cot C}{cot A cot B cot C}$ =
06:27
View Solution
Let $\to a = ˆ j - ˆ k$ and $\to c = ˆ i - ˆ j - ˆ k$ . Then vector $\to b$ satisfying $\to a \times \to b + \to c = \to 0$ and $\to a . \to b = 3$ is (1) $2 \to i - \to j + 2 \to k$ (2) $ˆ i - ˆ j - 2 ˆ k$ (3) $ˆ i + j - 2 ˆ k$ (4) $- ˆ i + ˆ j - 2 ˆ k$
03:40
View Solution
Find a unit vector perpendicular to both of the vectors $\to a + \to b$ and $\to a - \to b$ where $\to a = ˆ i + ˆ j + ˆ k, \to b = ˆ i + 2 ˆ j + 3 ˆ k .$
05:55
View Solution
If $\to a = ˆ i + 2 ˆ j + 3 ˆ k$ and $\to b = 2 ˆ i + 3 ˆ j + ˆ k$ , find a unit vector in the direction of $(2 \to a + \to b)$ .
06:37
View Solution
Find the unit vectors perpendicular to both $\to a$ and $\to b$ when
(i) $\to a = 3 ˆ i + ˆ j - 2 ˆ k$ and $\to b = 2 ˆ i + 3 ˆ j - ˆ k$
(ii) $\to a = ˆ i - 2 ˆ j + 3 ˆ k$ and $\to b = ˆ i + 2 ˆ j - ˆ k$
(iii) $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ and $\to b = - ˆ i + 3 ˆ k$
(iv) $\to a = 4 ˆ i + 2 ˆ j - ˆ k$ and $\to b = ˆ i + 4 ˆ j - ˆ k$
01:27
View Solution
Find the projection of vector $(\to b + \to a)$ on vector $\to a$ where $\to a = 2 ˆ i - ˆ j + 2 ˆ k and \to b = ˆ j + 2 ˆ k$
02:18
View Solution
सदिश $(\to a + \to b)$ और $(\to a - \to b)$ में से प्रत्येक के मात्रक सदिश ज्ञात कीजिए जहाँ $\to a = ˆ i + ˆ j + ˆ k, \to b = ˆ i + 2 ˆ j + 3 ˆ k$ है।
01:55
View Solution
Given $\to a = 4 ˆ i - ˆ j + 3 ˆ k$ and $\to b = - 2 ˆ i + ˆ j - 2 ˆ k$ .
(i) Find a unit vector perpendicular to both $\to a$ and $\to b$ .
(ii) Find a vector of magnitude 9 which is perpendicular to both $\to a$ and $\to b$ .
03:30
View Solution
For given vectors $\to a = 2 ˆ i - ˆ j + 2 ˆ k$ and $\to b = - ˆ i + ˆ j - ˆ k$ , find the unit vector in the direction of the vector $\to a + \to b$ .
06:39
View Solution
If $\to a = ˆ i + ˆ j + ˆ k$ , $\to b = 2 ˆ i - ˆ j + 3 ˆ k$ and $\to c = ˆ i - 2 ˆ j + ˆ k$ , find a unit vector parallel to the vector $2 \to a - \to b + 3 \to c$
02:57
View Solution
For given vector, $\to a$ = 2 $ˆ i$ $j$ +2 $ˆ k$ and $\to b$ = - $ˆ i$ + $ˆ j$ - $ˆ k$ , find the unit vector in the direction of the vector $\to a$ + $\to b$ .
05:39
View Solution
If $\to a = ˆ i + ˆ j + ˆ k, \to b = 2 ˆ i - ˆ j + 3 ˆ k a n d \to c = ˆ i - 2 ˆ j + ˆ k$ find a unit vector parallel to $2 \to a - \to b + 3 \to c$
04:54
View Solution
Let $\to a = ˆ j - ˆ k$ and $\to c = ˆ i - ˆ j - ˆ k$ . Then vector $\to b$ satisfying $\to a \times \to b + \to c = \to 0$ and $\to a . \to b = 3$ is (1) $2 \to i - \to j + 2 \to k$ (2) $ˆ i - ˆ j - 2 ˆ k$ (3) $ˆ i + j - 2 ˆ k$ (4) $- ˆ i + ˆ j - 2 ˆ k$
06:18
View Solution

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Find |vec a xx vec b| if vec a = hat i -7 hat j + 7 hat k and vec b = ...
02:08
Find a unit vector perpendicular to each of the vector vec a+ vec b a...
04:49
If a unit vector vec a makes angles(pi)/(3) with hat i , (pi)/(4) with...
14:53
Show that (vec a - vec b) xx (vec a + vec b) = 2 (vec a xx vec b)
01:20
Find lambda amd mu if (2 hat i + 6 hat j+ 27 hat k) xx (hat i + lambda...
01:48
Given that vec a. vec b = 0 and vec a xx vec b = vec 0. What can you c...
01:36
Let the vectors veca, vecb, vec c be given as a(1)hat i + a(2)hatj + a...
15:02
If either vec a = vec 0 or vec a xx vec b = vec 0 .Is the converse tr...
05:02
Find the area of the triangle with vertices A(1,1,2)B(2,3,5) and C(1,5...
01:52
Find the area of the parallelogram whose adjacent sides are determined...
02:38
Let the vectorsvec a and vec b be such that |veca| = 3 and |vecb| = (s...
01:58
Area of a rectangle having vertices A,B,C and D with positions vectors...
08:02

Home
Ask Doubt
Profile

Find a unit vector perpendicular to each of the vector →a+→b and →a−→b, where →a=3ˆi+2ˆj+2ˆk and →b=ˆi+2ˆj−2ˆk.Solution in Tamil

The correct Answer is:±(23ˆi−23ˆj−13ˆk)

Topper's Solved these Questions

Similar Questions

NEW JOYTHI PUBLICATION-VECTOR ALGEBRA-SOLUTIONS TO NCERT TEXT BOOK EXERCISE 10.4

Find a unit vector perpendicular to each of the vector $\to a + \to b$ and $\to a - \to b$ , where $\to a = 3 ˆ i + 2 ˆ j + 2 ˆ k$ and $\to b = ˆ i + 2 ˆ j - 2 ˆ k$ .Solution in Tamil

The correct Answer is: $\pm (\frac{2}{3} ˆ i - \frac{2}{3} ˆ j - \frac{1}{3} ˆ k)$