Find m∠C in fig 3.33 if AB∣∣DC
To find the measure of angle C in the given figure where AB is parallel to DC, we can follow these steps:
Step 1: Understand the properties of parallel lines
When two lines are parallel, the angles formed by a transversal line intersecting them have specific relationships. In this case, since AB is parallel to DC, we can use the properties of corresponding angles or alternate interior angles.
Step 2: Identify the angles
From the problem, we know that angle C is one of the angles formed by the transversal intersecting the parallel lines AB and DC. We are also given that there is another angle, which we will assume is 120 degrees.
Step 3: Use the angle sum property
According to the properties of parallel lines, the sum of the angles on the same side of the transversal is equal to 180 degrees. Therefore, we can set up the equation:
Angle C+120∘=180∘
Step 4: Solve for angle C
Now, we can isolate angle C:
Angle C=180∘−120∘
Angle C=60∘
Conclusion
Thus, the measure of angle C is 60 degrees.
---
When two lines are parallel, the angles formed by a transversal line intersecting them have specific relationships. In this case, since AB is parallel to DC, we can use the properties of corresponding angles or alternate interior angles.
From the problem, we know that angle C is one of the angles formed by the transversal intersecting the parallel lines AB and DC. We are also given that there is another angle, which we will assume is 120 degrees.
According to the properties of parallel lines, the sum of the angles on the same side of the transversal is equal to 180 degrees. Therefore, we can set up the equation:
Now, we can isolate angle C:
Thus, the measure of angle C is 60 degrees.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.1
2 Videos
- UNDERSTANDING QUADRILATERALSBOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.1
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
Knowledge Check
In a trapezium ABCD, AB||DC, AB = AD, ∠ADC=64∘and∠BCD=54∘. Find ∠DBC.
 A64∘B72∘C94∘D116∘
A64∘B72∘C94∘D116∘In a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
A36∘B72∘C108∘D144∘
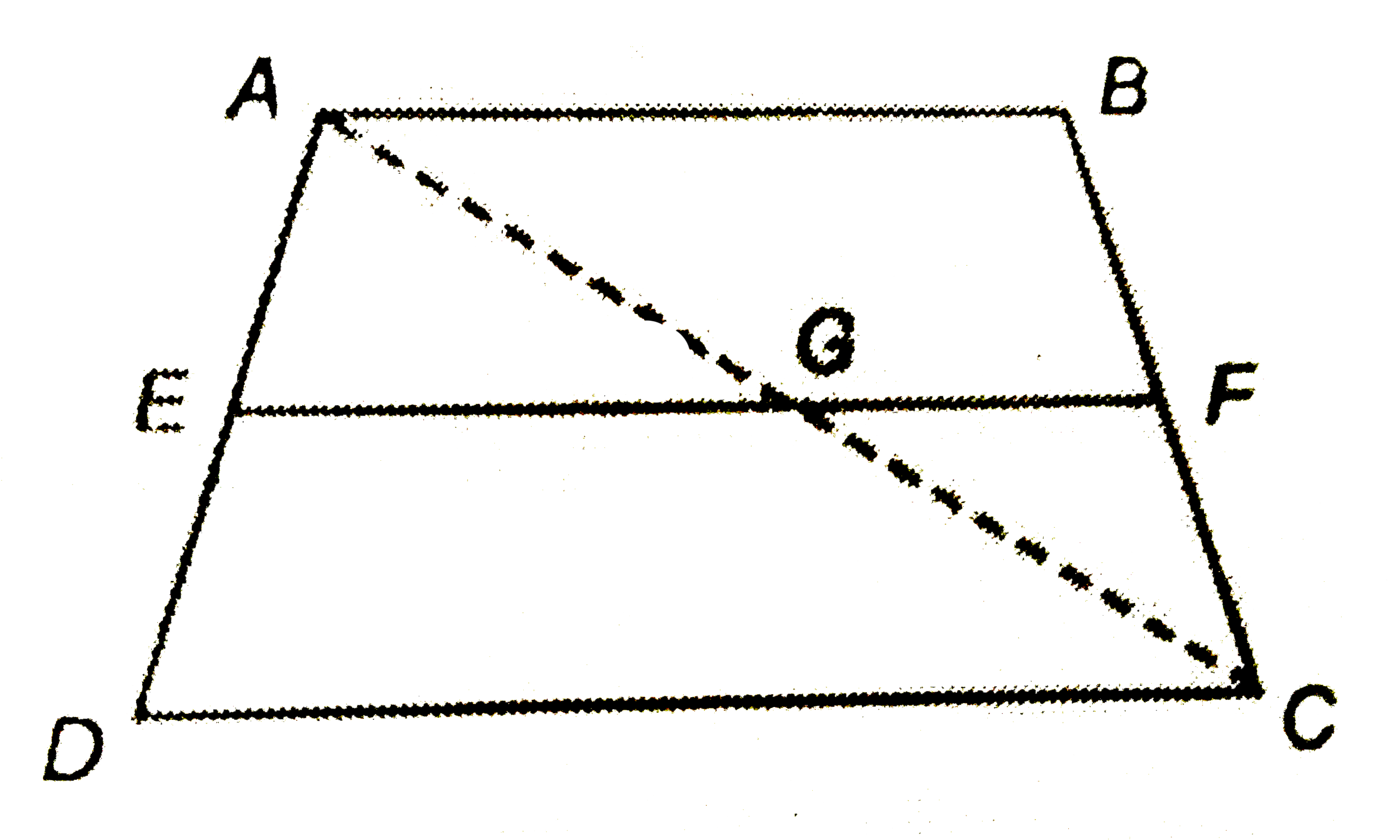
In the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
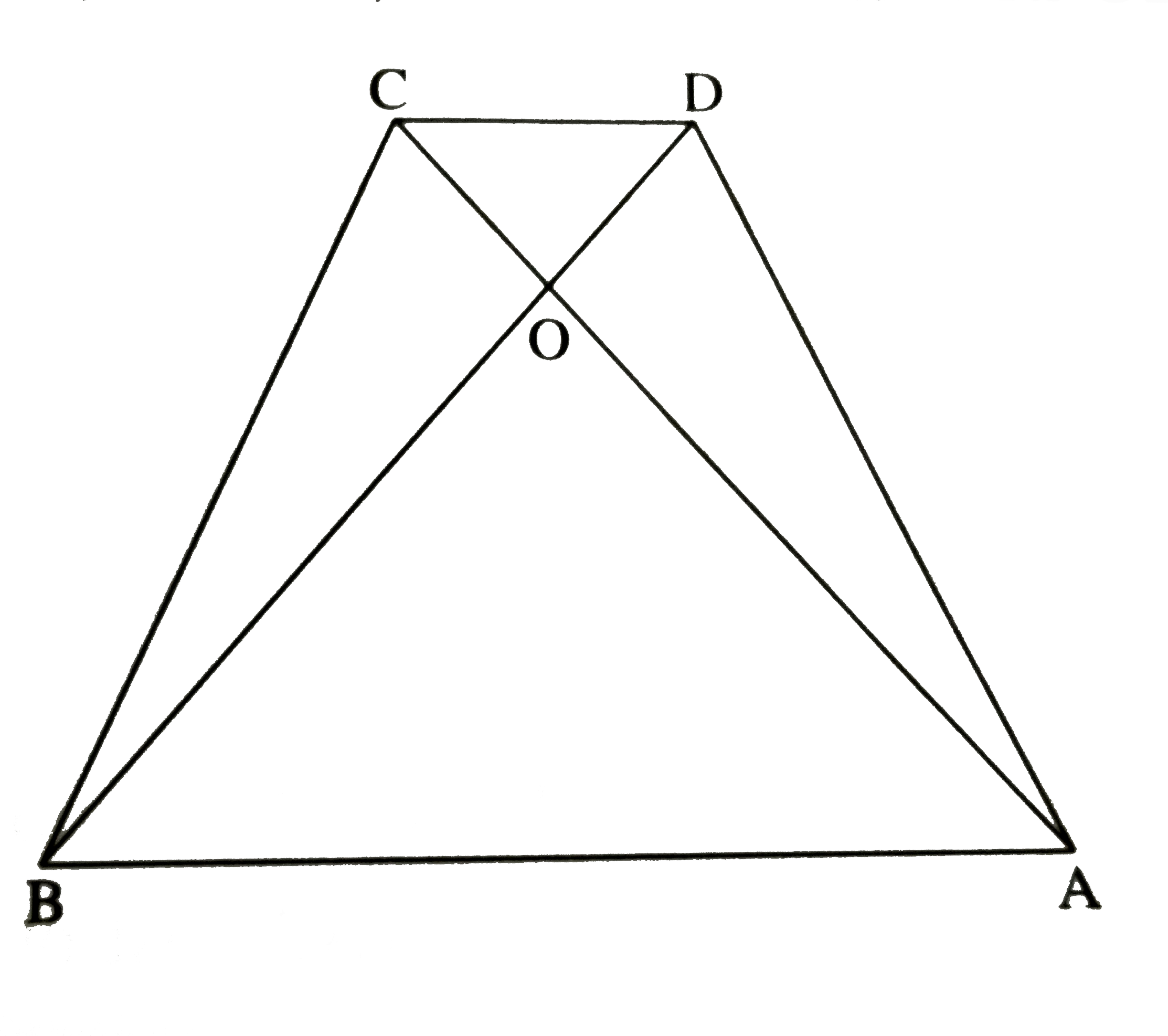
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionWill the lenghts of line segment AB and line segment BC make the length of line segment AC in Fig. 2.33 ?

View SolutionIn trapezium ABCD side AB∣∣ side DC, diagonals AC and BD intersect In point O. If AB=20,DC=6,OB=15 thn find OD.
View SolutionIn a triangle ABC, if ∠A=70∘andAB=AC, then find the measures of ∠Band∠C.
View SolutionABCD is a parallelogram. Angle bisector of ∠A and angle bisector of ∠C cuts extended side DC and AB at Q and P respectively. If ∠A=50∘, find ∠P+∠Q.
View Solution

