Find m∠C in fig 3.33 if AB∣∣DC
To find m∠C in the given figure where AB∥DC, we can follow these steps:
1. Identify the Given Information:
- We know that AB is parallel to DC.
- BC acts as a transversal line that intersects the two parallel lines.
Hint: Remember that when two lines are parallel, the angles formed by a transversal have special relationships.
2. Recognize the Angle Relationship:
- Since AB∥DC and BC is the transversal, we can identify ∠B and ∠C as co-interior angles (also known as consecutive interior angles).
Hint: Co-interior angles are located on the same side of the transversal and between the two parallel lines.
3. Apply the Co-Interior Angles Theorem:
- The sum of co-interior angles is equal to 180∘. Therefore, we can write the equation:
∠B+∠C=180∘
Hint: This theorem is crucial for solving problems involving parallel lines and transversals.
4. Substitute the Known Value:
- We are given that ∠B=120∘. Substitute this value into the equation:
120∘+∠C=180∘
Hint: Make sure to keep track of the angles and their relationships.
5. Solve for ∠C:
- Rearranging the equation gives:
∠C=180∘−120∘
- Calculate:
∠C=60∘
Hint: Always double-check your arithmetic when calculating angles.
6. Conclusion:
- Therefore, the measure of ∠C is 60∘.
Final Answer:
m∠C=60∘
- We know that AB is parallel to DC.
- BC acts as a transversal line that intersects the two parallel lines.
- Since AB∥DC and BC is the transversal, we can identify ∠B and ∠C as co-interior angles (also known as consecutive interior angles).
- The sum of co-interior angles is equal to 180∘. Therefore, we can write the equation:
∠B+∠C=180∘
- We are given that ∠B=120∘. Substitute this value into the equation:
120∘+∠C=180∘
- Rearranging the equation gives:
∠C=180∘−120∘
- Calculate:
∠C=60∘
- Therefore, the measure of ∠C is 60∘.
m∠C=60∘
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.4
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
Knowledge Check
The velocity time graph of a body is shown in fig. 3.3. it implies that at point B
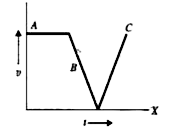 Athe force is zeroBthere is a force towards motionCthere is force which oppose motionDnone of the above
Athe force is zeroBthere is a force towards motionCthere is force which oppose motionDnone of the above
In triangle ABC,∠C=2π3andCD is the internal angle bisector of ∠C meeting the side AB at D. If Length CD is 1, then H.M. of aandb is equal to : (a) 1 (b) 2 (c) 3 (d) 4
View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionThe following figure shows a quadrilateral in which sideo AB and DC are parallel. If ∠A:∠D=4:5,∠B=(3x−15)∘and∠C=(4x+20)∘, find each angle of the quadrilateral ABCD.

View SolutionIn the given figure ABCD is a trapezium, P is the mid-point of side AD and PR||AB||DC.
Find the length of PR, if AB=12cmandDC=8cm
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC. If ∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrialateral ABCD.
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionIn △ABCifABAC=BDDCandif∠B=70∘and∠C=50∘f∈d∠BAD
View Solution