Find the area bounded by the curve xy2=4(2−x) and y-axis.
Video Solution
Text Solution
The correct Answer is:4π sq. units
We have curve xy2=4(2−x)
∴ x=8y2+4
The given curve is symmetrical about x-axis and meets it at (2,0).
Also, when y→±∞,x→0.
So, y-axis is asymptote to the curve.
The graph of the function is as shown in the following figure.
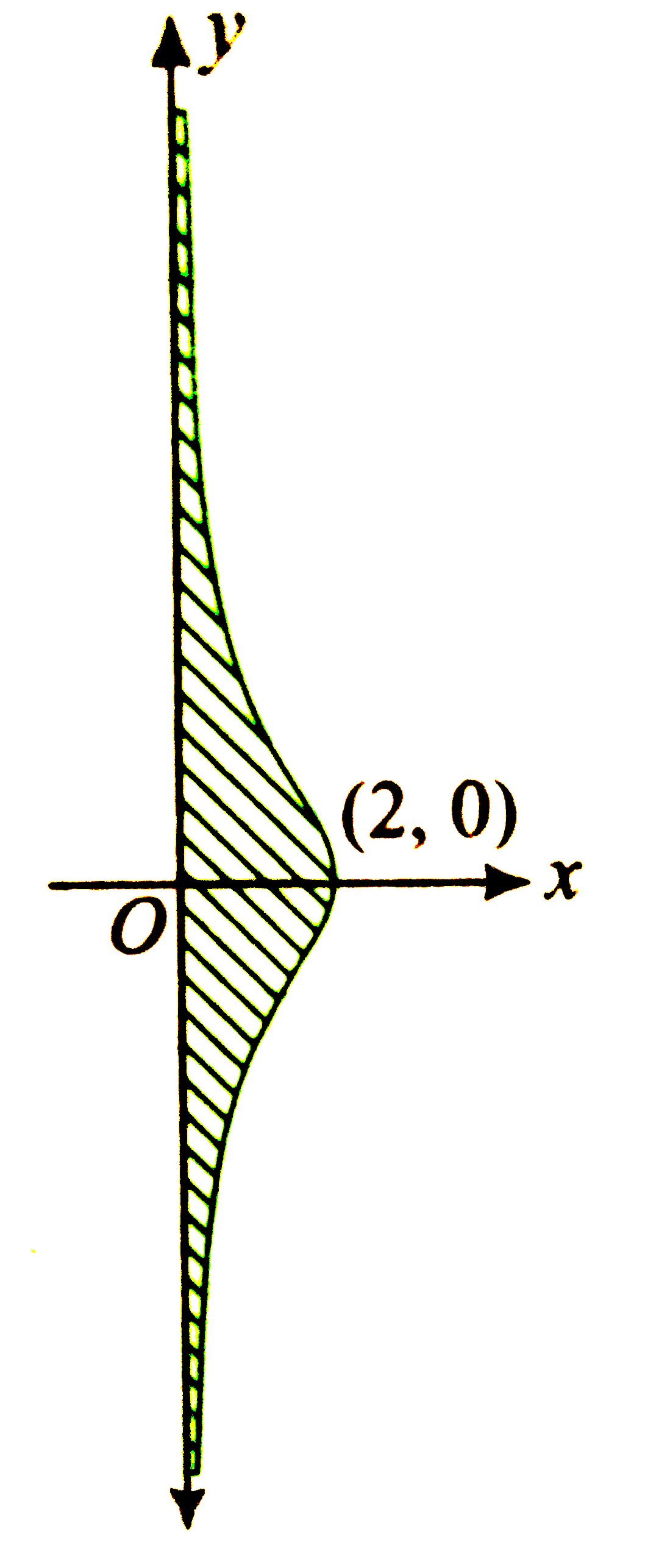
The line x=0, i.e., y-axis is asymptote.
Area of the shaded region =2∫∞08y2+4dx
=16[12tan−1y2]∞0=8×π2
=4π sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Comprehension Type
2 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
the area included between the curve xy2=a2(a−x) and y -axis is -
Aπa2/2Bπa2C3πa2DNoneThe area bounded by the curve x=2−y−y2 and Y-axis is
A32 sq unitsB52 sq unitsC92 sq unitsDNone of theseThe area bounded by the curve y=x(x2−1) and x-axis is
A0B12C1D14
Find the area bounded by the curve y2=4ax and x2+y2−2ax=0 above the x-axis.
View SolutionExamples: Find the area of the region bounded by the curve y2=2y−x and the y-axis.
View SolutionFind the area bounded by the curves : y2=4x,y2=x,x=1andx=4
View SolutionFind the area bounded by the curves x2=y, x2=−y and y2=4x−3
View SolutionFind area bounded by the curves x2≤y≤x+2
View Solution
