Find the area bounded by the curves y=s∈xandy=cosx between two consecutive points of the intersection.Solution in Tamil
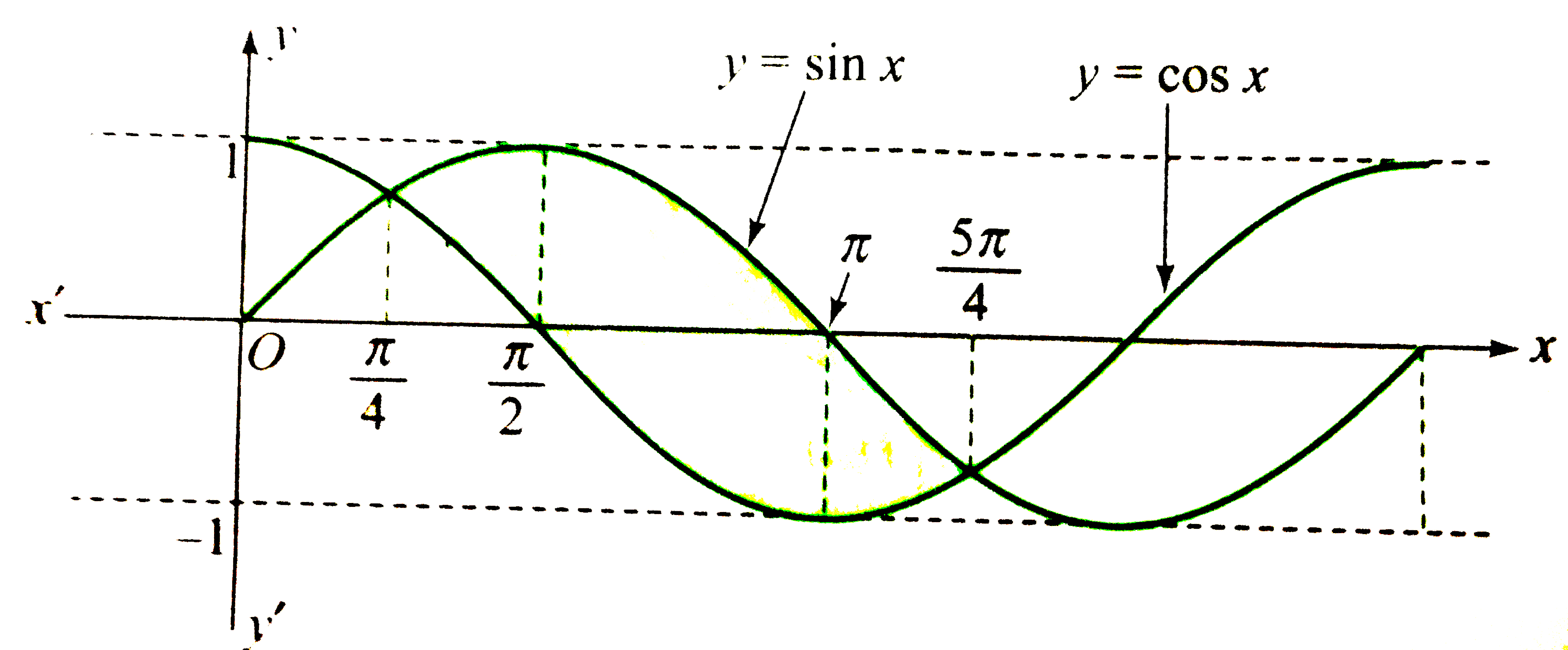
Two consecutive points of intersection of y=sinxandy=cosx can be taken as x=π/4andx=5π/4. Therefore,
Required area =∫5π/4π/4(sinx−cosx)dx
=[−cosx−sinx]5π/4π/4
=2√2+2√2
=2√2 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area bounded by the curves y=s∈xandy=cosx between two consecutive points of the intersection.
View SolutionFind the area bounded by y=sinx and y=cosx between any two consecutive points of intersection.
View SolutionFind the area bounded by the curves y=sinx and y=cos x between two consecutive points of their intersection.
View Solutiony=sinx এবং y=cosx এই বক্ররেখা দুটির পরপর যে-কোনো দুটি ছেদবিন্দুর মধ্যবর্তী এবং বক্ররেখা দুটি দ্বারা সীমাবদ্ধ অঞ্চলের ক্ষেত্রফল নির্ণয় করো।
View SolutionFind the angle of intersection of y=axandy=bx
View SolutionCompute the area of the region bounded by the curves y=ex(log)exandy=logxex
View SolutionFind the area bounded by the curves y=sin x and y=cos x between two consecutive points of the intersection.
View SolutionFind the area bounded by the curves y=sinxandy=cosx between two consecutive points of the intersection.
View SolutionCompute the area of the region bounded by the curves y−ex(log)exandy=logxex
View SolutionThe area bounded by the curves y=(log)exandy=((log)ex)2 is
View SolutionFind the area bounded by the curves y=xandy=x3.
View Solution
