Find the area bounded by the curves y=sin x and y=cos x between two consecutive points of the intersection.Solution in Bengali
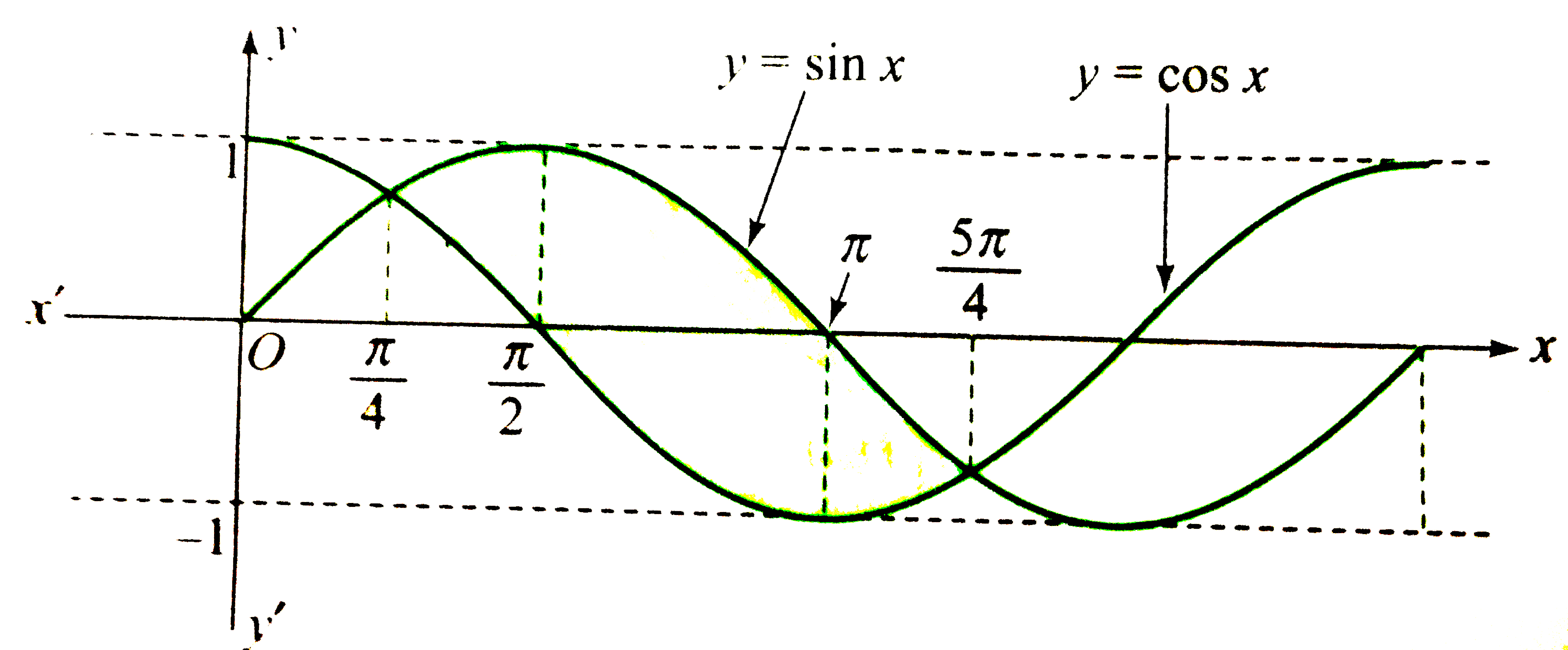
Two consecutive points of intersection of y=sinxandy=cosx can be taken as x=π/4andx=5π/4. Therefore,
Required area =∫5π/4π/4(sinx−cosx)dx
=[−cosx−sinx]5π/4π/4
=2√2+2√2
=2√2 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionFind the area bounded by the curves y=s∈xandy=cosx between two consecutive points of the intersection.
View SolutionConsider the curves y=sin x and y=cos x. What is the area of y=sin x bounded by the above two curves the region bounded by the above two curves and the lines x=0 and x=(pi)/(4)
View SolutionThe area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = (3pi)/(2) , is
View SolutionFind the area bounded by y=sinx and y=cosx between any two consecutive points of intersection.
View SolutionThe area enclosed between the curves y=sin2x y=cos2x in 0<x<π and between their consecutive points of intersection is
View SolutionFind the area bounded by the curves y=sinx and y=cos x between two consecutive points of their intersection.
View SolutionThe area bounded by the curves y=cos x and y=sin x between the ordinates x=0 and x=3/2pi is :
View SolutionConsider the curves y2=x and x2=y.
(i) Find the points of intersection of these two curves.
(ii) Find the area between these two curves.
View SolutionFind the area bounded by the curves y=sin x and y=cos x between two consecutive points of the intersection.
View SolutionFind the area bounded by the curves y=sinxandy=cosx between two consecutive points of the intersection.
View SolutionThe area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = (3pi)/(2) , is
View Solutiony=sinx and y=cosx intersect at many points.If area enclosed by them between two consecutive intersection points is A find A4.
View Solution
