Find the area enclosed between the curves: y=loge(x+e),x=loge(1y) & the x-axis. Solution in Tamil
2 sq. units
1 sq. units
4 sq. units
None of these
The correct Answer is:A
y=loge(x+e),x=loge(1y)ory=e−x.
For y=loge(x+e), Shift the graph of y=logex,e units to the left hand side.
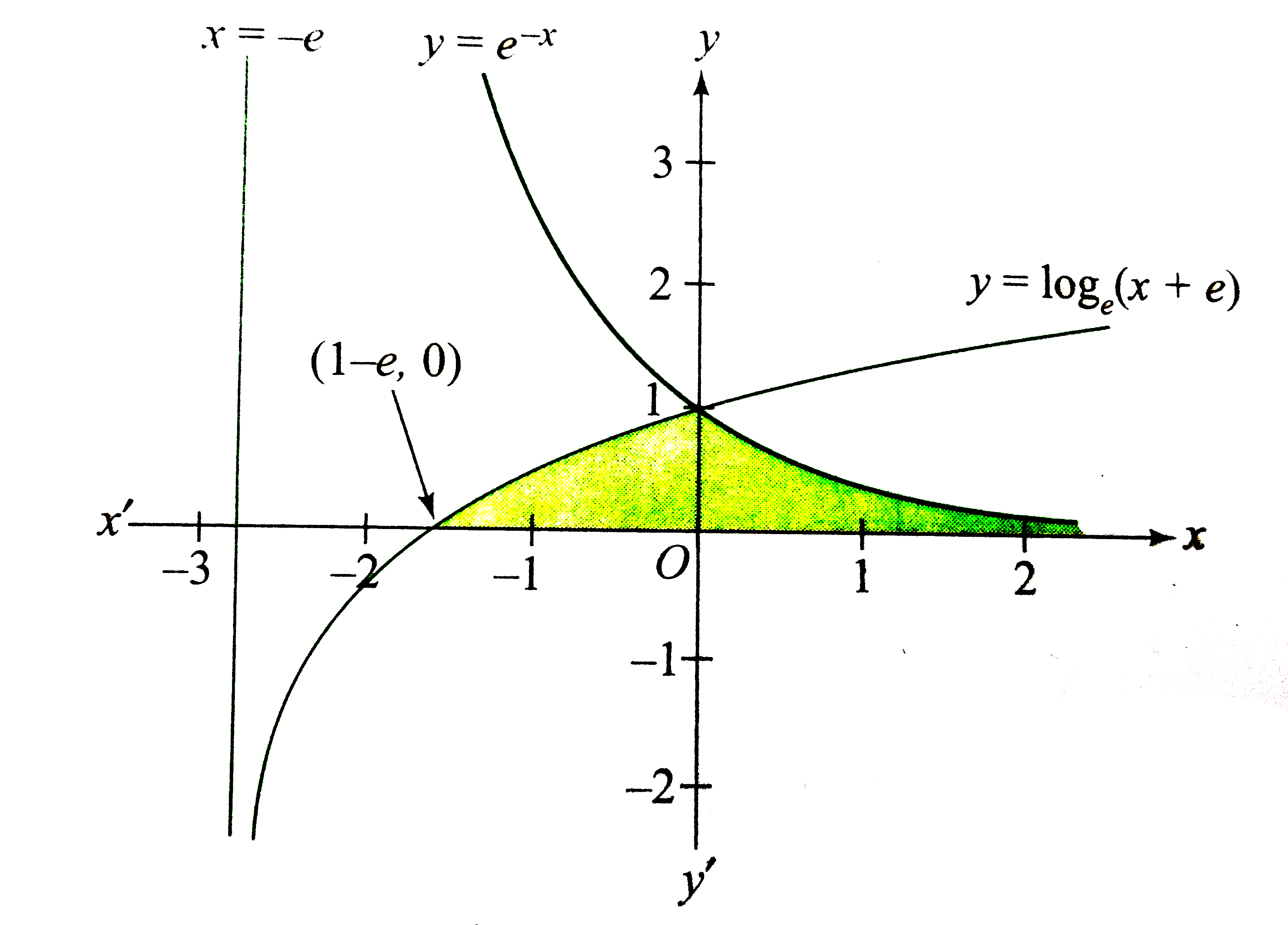
Required area =0∫1−eloge(x+e)dx+∞∫0e−xdx
=|xloge(x+e)|01−e−0∫1−exx+edx−∣∣e−x∣∣∞0
=1−e∫0(1−ex+e)dx−e∞+e0
=|x−elog(x+e)|1−e0−0+1
=1−e+eloge+1=2 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)
21 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionFind the area enclosed between the curves: y=log_(e)(x+e),x=log_(e)((1)/(y))& the x -axis.
View SolutionFind the area enclosed by the graph of y=loge(x+1),y-axis, and the line y=1
View Solutionवक्र y=logex, X-अक्ष तथा कोटियों x = 1 तथा x = e से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र y=logex,x−अक्ष तथा कोटि x=e द्वारा परिबद्ध क्षेत्रफल है :
View Solutionवक्र y=loge(x+e) तथा अक्षों से परिबद्ध क्षेत्रफल का मान है
View SolutionThe area enclosed between the curve y=loge(x+e) and the coordinate axes is :
View SolutionFind the area enclosed by y=loge(x+e) and x=loge(1y) and the x-axis.
View SolutionThe area encosed between the curves y=loge(x+e),y=ex and the X-axis is
View SolutionFind the area enclosed by the graph of y=loge(x+1),y-axis, and the line y=1
View SolutionFind the area enclosed between the curves: y=loge(x+e),x=loge(1y) & the x-axis.
View SolutionCoordinates and curves y = log_(e)x Is the area enclosed by
View Solution
