Find the area if the region bounded by $y = \sqrt{x} and y = x$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

Given equation of curves are $y = \sqrt{x} and y = x$ .
$\Rightarrow x = \sqrt{x} \Rightarrow x^{2} = x$
$\Rightarrow x^{2} - x = 0 \Rightarrow x (x - 1) = 0$
$\Rightarrow x = 0.1$

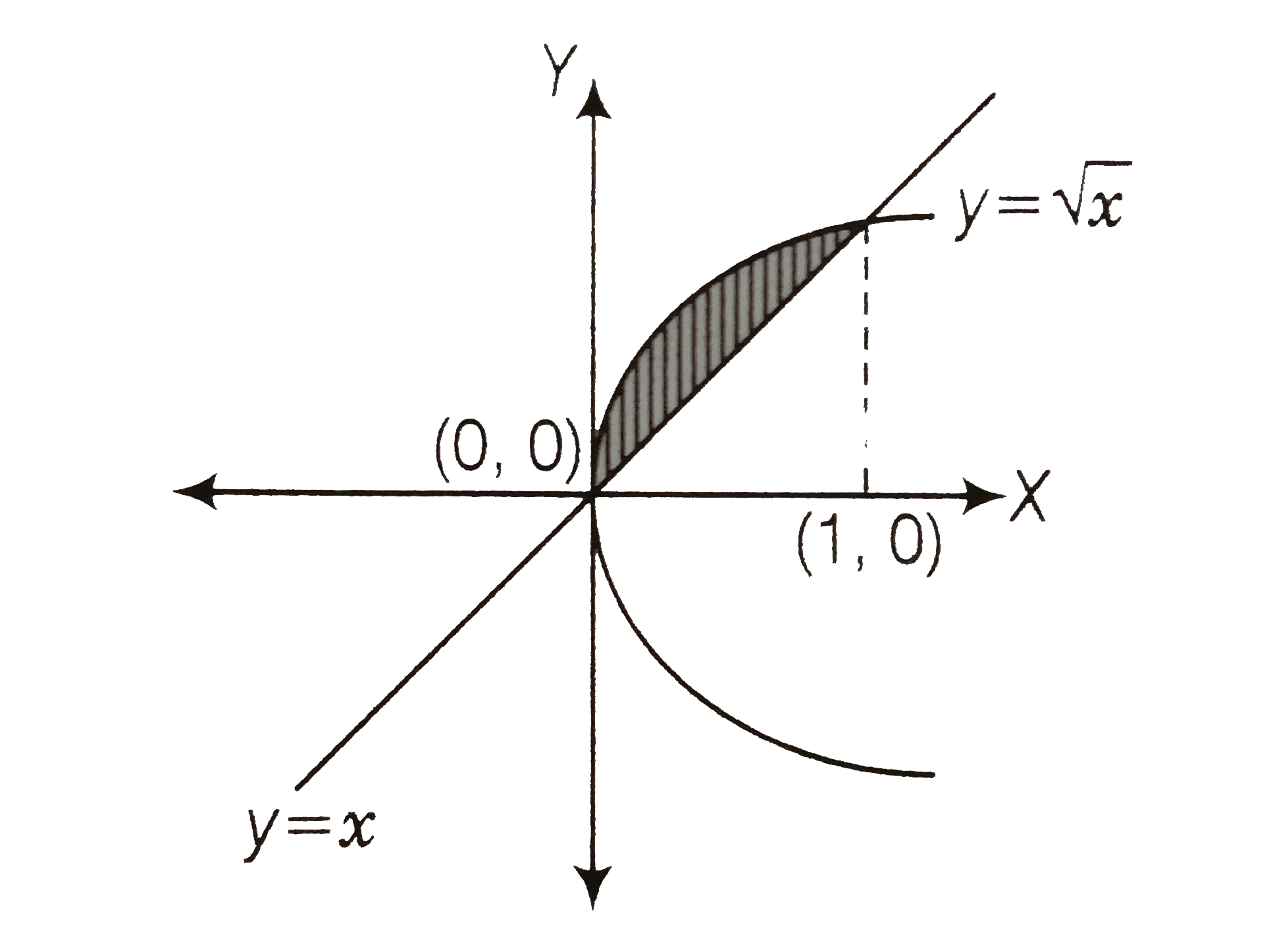
$∴ Required area of shaded region, A = \int_{0}^{1} (\sqrt{x}) d x - \int_{0}^{1} x d$
$= {[2 . \frac{x^{3 / 2}}{3}]}_{0}^{1} - {[\frac{x^{2}}{2}]}_{0}^{1}$
$= \frac{2}{3} .1 - \frac{1}{2} = \frac{2}{3} - \frac{1}{2} = \frac{1}{6} sq units$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Objective Type Questions

Home
Ask Doubt
Profile