Find the area of the hexagon shown in Figure if MP=9 cm,MD=7 cm,MC=6 cm,MB=4 cm,MA=2 cm NA,OC,QD and RB are perpendiculars to diagonal MP.
To find the area of the hexagon with the given dimensions, we will break down the hexagon into triangles and trapeziums. Here’s the step-by-step solution:
Step 1: Identify the dimensions
Given:
- MP = 9 cm
- MD = 7 cm
- MC = 6 cm
- MB = 4 cm
- MA = 2 cm
We also know that NA, OC, QD, and RB are perpendiculars to diagonal MP.
Step 2: Calculate the segments
We need to find the lengths of the segments:
1. AB = MB - MA = 4 cm - 2 cm = 2 cm
2. AC = MC - MA = 6 cm - 2 cm = 4 cm
3. BD = MD - MB = 7 cm - 4 cm = 3 cm
4. CP = MP - MC = 9 cm - 6 cm = 3 cm
5. DP = MP - MD = 9 cm - 7 cm = 2 cm
Step 3: Calculate the areas of the triangles and trapeziums
The area of the hexagon can be calculated as the sum of the areas of the triangles and trapeziums formed.
1. Area of Triangle MNA:
- Base = AB = 2 cm
- Height = NA = 2.5 cm (assumed height)
- Area = 12×Base×Height=12×2×2.5=2.5cm2
2. Area of Trapezium ANOC:
- Parallel sides = AC = 4 cm and NO = 3 cm (assumed)
- Height = OC = 2.5 cm
- Area = 12×(Base1+Base2)×Height=12×(4+3)×2.5=8.75cm2
3. Area of Trapezium BRQD:
- Parallel sides = BD = 3 cm and RQ = 2 cm (assumed)
- Height = QD = 3 cm
- Area = 12×(3+2)×3=7.5cm2
4. Area of Triangle MBP:
- Base = CP = 3 cm
- Height = RB = 2 cm (assumed)
- Area = 12×3×2=3cm2
Step 4: Sum the areas
Now, we sum all the areas calculated:
- Total Area = Area of MNA + Area of ANOC + Area of BRQD + Area of MBP
- Total Area = 2.5+8.75+7.5+3=22.75cm2
Final Answer
The area of the hexagon is 22.75 cm².
---
Given:
- MP = 9 cm
- MD = 7 cm
- MC = 6 cm
- MB = 4 cm
- MA = 2 cm
We need to find the lengths of the segments:
1. AB = MB - MA = 4 cm - 2 cm = 2 cm
2. AC = MC - MA = 6 cm - 2 cm = 4 cm
3. BD = MD - MB = 7 cm - 4 cm = 3 cm
4. CP = MP - MC = 9 cm - 6 cm = 3 cm
5. DP = MP - MD = 9 cm - 7 cm = 2 cm
The area of the hexagon can be calculated as the sum of the areas of the triangles and trapeziums formed.
- Base = AB = 2 cm
- Height = NA = 2.5 cm (assumed height)
- Area = 12×Base×Height=12×2×2.5=2.5cm2
- Parallel sides = AC = 4 cm and NO = 3 cm (assumed)
- Height = OC = 2.5 cm
- Area = 12×(Base1+Base2)×Height=12×(4+3)×2.5=8.75cm2
- Parallel sides = BD = 3 cm and RQ = 2 cm (assumed)
- Height = QD = 3 cm
- Area = 12×(3+2)×3=7.5cm2
- Base = CP = 3 cm
- Height = RB = 2 cm (assumed)
- Area = 12×3×2=3cm2
Now, we sum all the areas calculated:
- Total Area = Area of MNA + Area of ANOC + Area of BRQD + Area of MBP
- Total Area = 2.5+8.75+7.5+3=22.75cm2
The area of the hexagon is 22.75 cm².
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions
110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions
134 Videos
Similar Questions
Find the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
View SolutionFind the area of rhombus whose diagonals are :
(i) 12 cm , 21 cm
(ii) 17.8 cm , 25 cm
View SolutionFind the area of a rectangle of dimensions 4.7 cm and 5.8cm.
View SolutionFind the surface area of the sphere whose radius is :
(a) 7 cm
(b) 3.5 cm
(c ) 1 cm
View SolutionFind the area of a triangle :
whose height is 6 cm and base is 10 cm.
View SolutionFind the area of a quadrilateral which has one diagonal measuring 22 cm, and the perpendiculars from the opposite vertices on this diagonal are 6 cm and 10 cm, respectively.
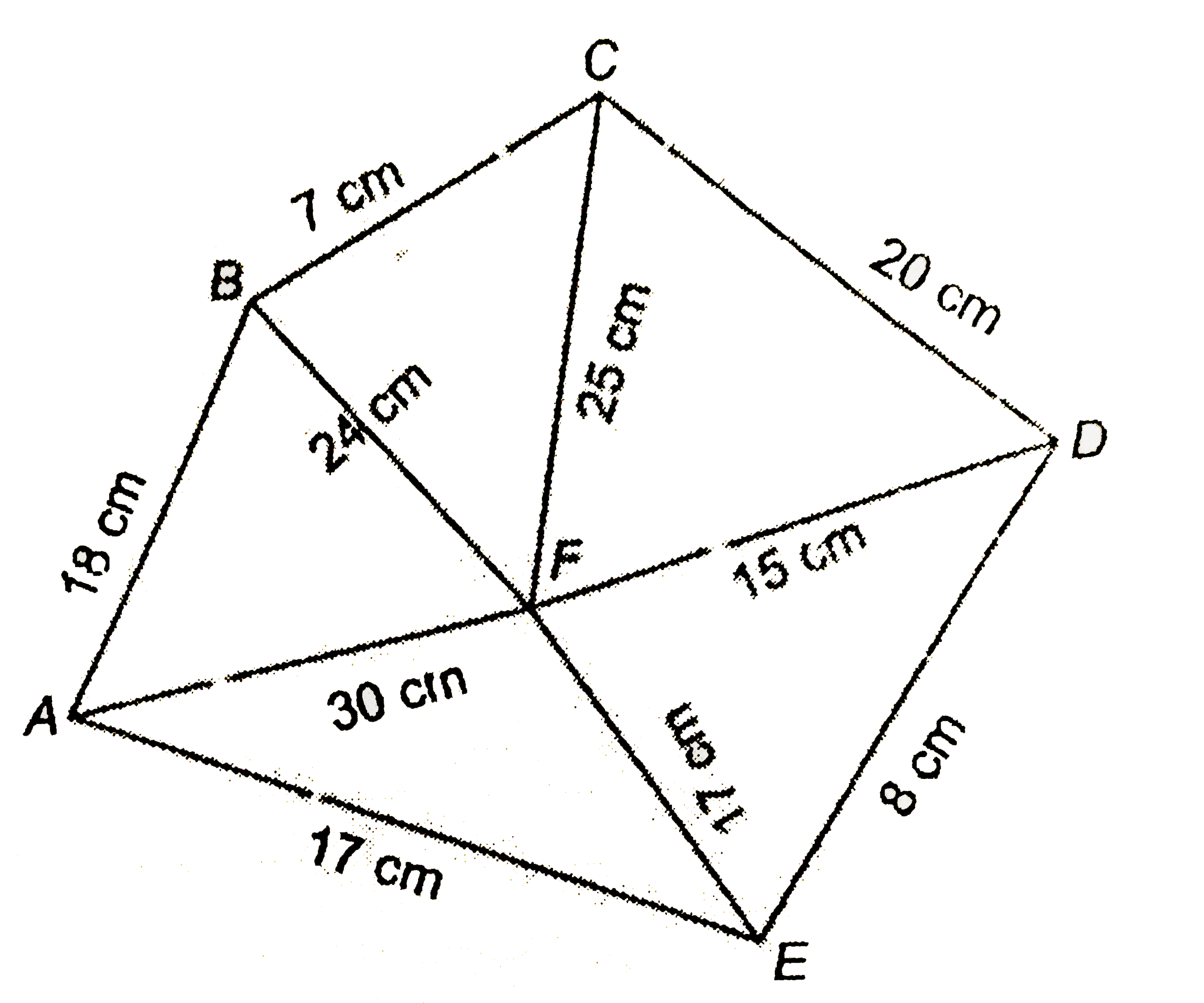
View SolutionFind the area of the given figure
Given AB = 18 cm, BC = 7 cm, CD = 20 cm, DE = 8 cm, EA = 17 cm, AF = 30 cm, BF = 24 cm, CF = 25 cm, FD = 15 cm, EF = 17 cm.
View SolutionFind the area of the rhombus , the lengths of whose diagonals are 17.5 cm and 22.4 cm.
View SolutionFind the area of a quadrilateral one of whose diagonal, is 25 cm long and the perpendicular from the other two vertices to this diagonal are 10 cm and 12 cm.
View Solution
