Find the area of the pentagonal park shown in Figure in two different ways:
To find the area of the pentagonal park in two different ways, we can follow these steps:
Method 1: Dividing the Pentagon into Two Trapeziums
1. Identify the Dimensions:
- The lengths of the parallel sides of the trapezium are given as 30 meters and 15 meters.
- The height (distance between the parallel sides) is half of 15 meters, which is 7.5 meters.
2. Calculate the Area of Each Trapezium:
- The formula for the area of a trapezium is:
Area=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height.
- For the first trapezium:
Area=12×(30+15)×7.5
=12×45×7.5
=22.5×7.5=168.75 m2
- Since there are two trapeziums, we multiply the area of one trapezium by 2:
Total Area=2×168.75=337.5 m2
Method 2: Dividing the Pentagon into a Triangle and a Rectangle
1. Identify the Dimensions:
- The base of the triangle is 15 meters.
- The height of the triangle is also 15 meters (the height from the base to the top vertex).
- The rectangle has both length and breadth as 15 meters.
2. Calculate the Area of the Triangle:
- The formula for the area of a triangle is:
Area=12×base×height
- For the triangle:
Area=12×15×15
=12×225=112.5 m2
3. Calculate the Area of the Rectangle:
- The area of the rectangle is given by:
Area=length×breadth
- For the rectangle:
Area=15×15=225 m2
4. Add the Areas Together:
- Total area of the pentagon:
Total Area=Area of Triangle+Area of Rectangle
=112.5+225=337.5 m2
Conclusion
In both methods, the area of the pentagonal park is found to be:
Area=337.5 m2
- The lengths of the parallel sides of the trapezium are given as 30 meters and 15 meters.
- The height (distance between the parallel sides) is half of 15 meters, which is 7.5 meters.
- The formula for the area of a trapezium is:
Area=12×(a+b)×h
where a and b are the lengths of the parallel sides, and h is the height.
- For the first trapezium:
Area=12×(30+15)×7.5
=12×45×7.5
=22.5×7.5=168.75 m2
- Since there are two trapeziums, we multiply the area of one trapezium by 2:
Total Area=2×168.75=337.5 m2
- The base of the triangle is 15 meters.
- The height of the triangle is also 15 meters (the height from the base to the top vertex).
- The rectangle has both length and breadth as 15 meters.
- The formula for the area of a triangle is:
Area=12×base×height
- For the triangle:
Area=12×15×15
=12×225=112.5 m2
- The area of the rectangle is given by:
Area=length×breadth
- For the rectangle:
Area=15×15=225 m2
- Total area of the pentagon:
Total Area=Area of Triangle+Area of Rectangle
=112.5+225=337.5 m2
In both methods, the area of the pentagonal park is found to be:
Area=337.5 m2
Topper's Solved these Questions
- LINEAR EQUATION IN ONE VARIABLEBook:RD SHARMA ENGLISHChapter:LINEAR EQUATION IN ONE VARIABLEExercise:All Questions
Explore 110 Videos
- MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)Book:RD SHARMA ENGLISHChapter:MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)Exercise:All Questions
Explore 134 Videos
Similar Questions
Find the area of the given figure.
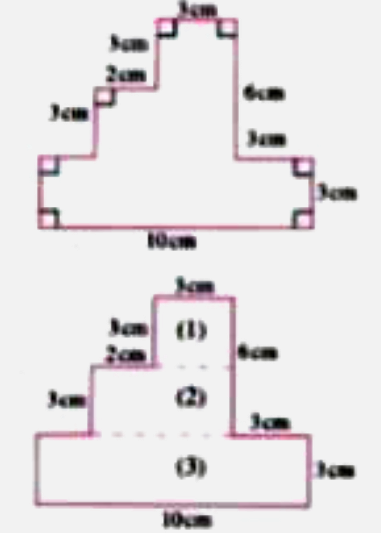
View SolutionFind the area of the given figure.
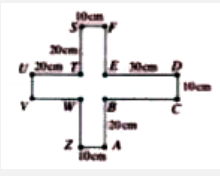
View SolutionFind the area of the shape shown in the figure 10.10.
View SolutionFind the area of the following figures

View SolutionFind the area of the following figures.
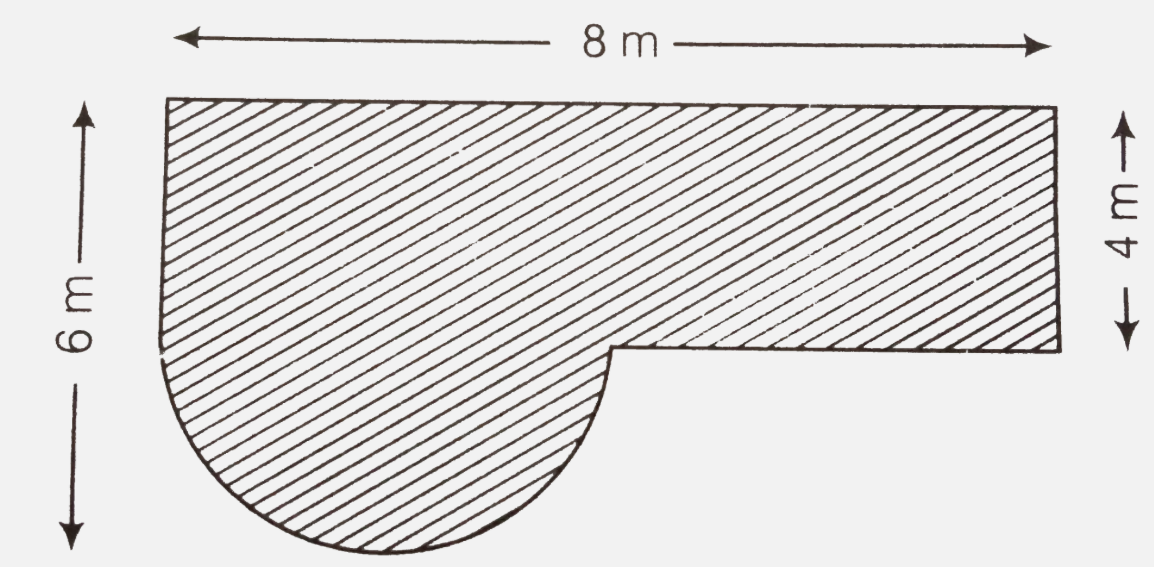
View SolutionFind the area of the shaded field shown in figure.
View SolutionFind the area of the field shown in Figure by dividing it into a square, a rectangle and a trapezium.
View SolutionFind the area of the pentagon shown in Figure, if AD=10cm, AG=8cm, AH=6cm, AF=5cm, BF=5cm, CG=7cm and EH=3cm.
View SolutionFind the area of the blades of the magnetic compass as shown in figure
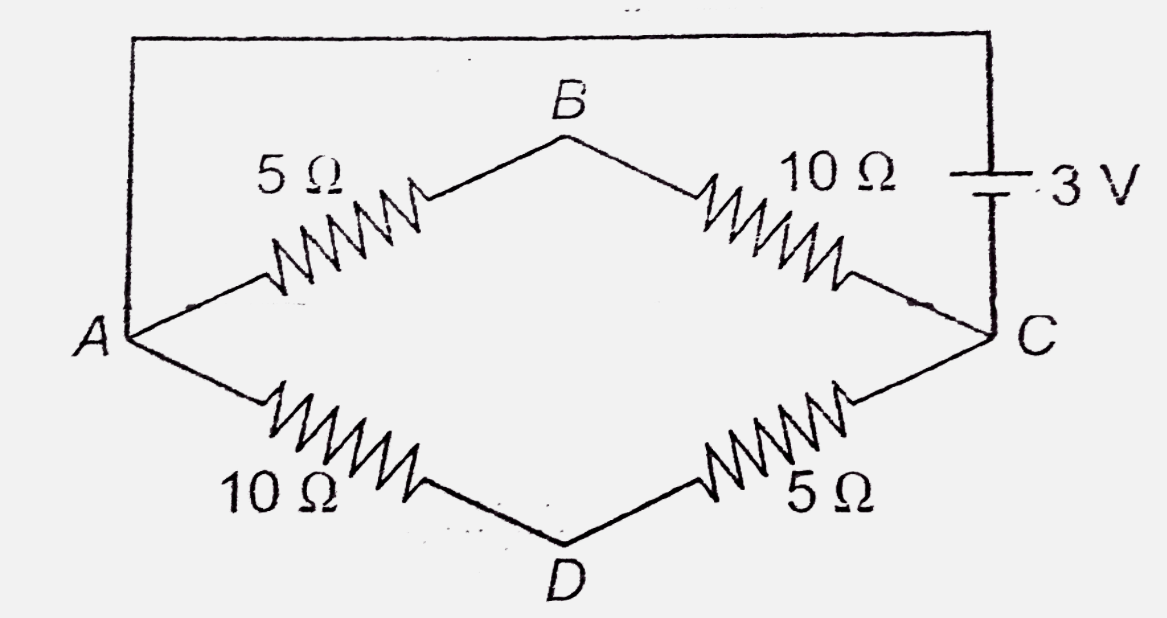
View SolutionIn the network shown in given figure, find the potential difference across BD
View Solution