Find the area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣,andyl=2, which lies to the right of the line x=1.
The given curves are
y=x2 (1)
y=∣∣2−x2∣∣ (2)
The graphs of these curve are as follows :
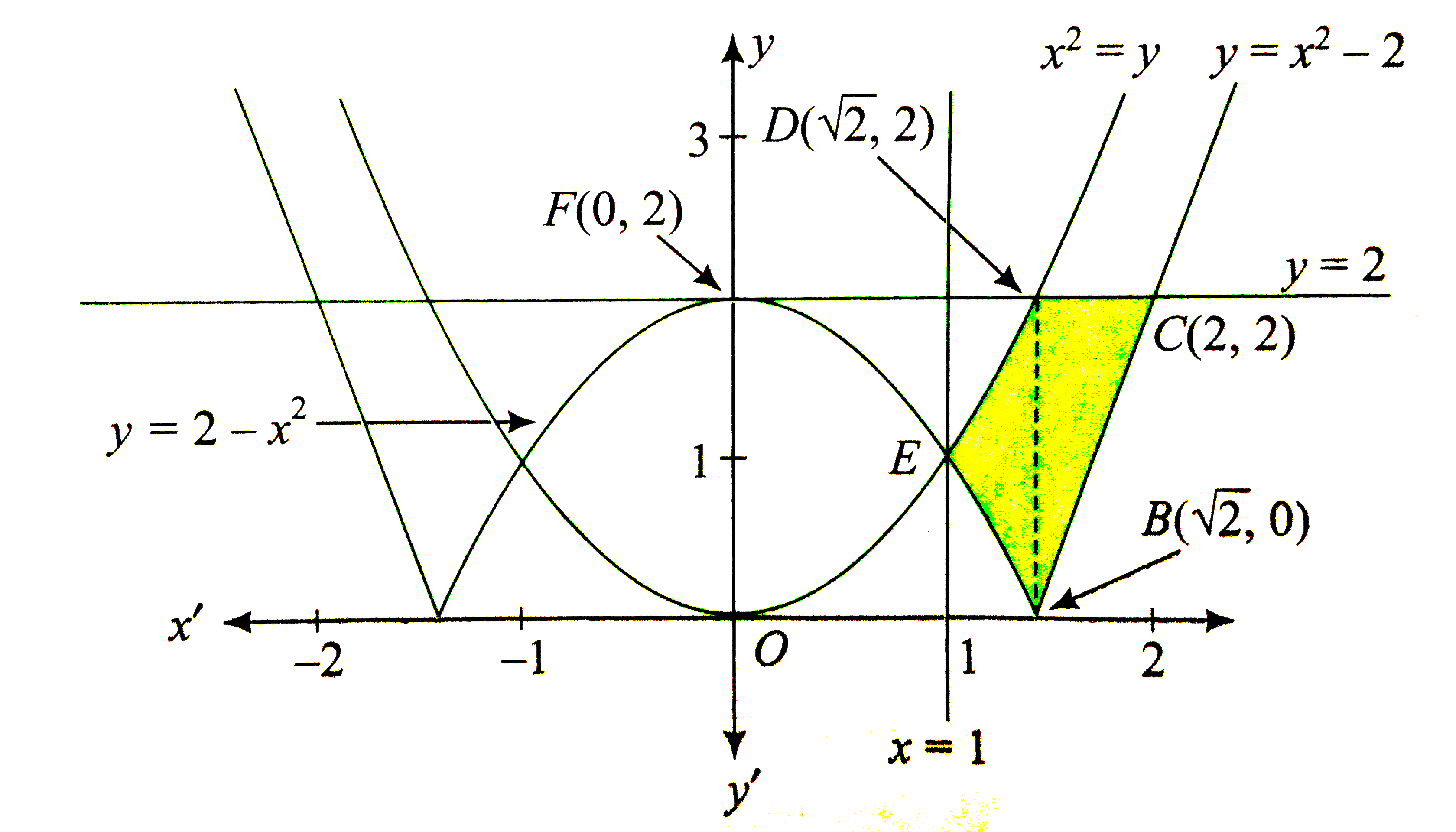
∴ Required area =BCDEB
=∫√21[x2−(2−x2)]dx+∫2√2[2−(x2−2)]dx
=∫√21(2x2−2)dx+∫2√2(4−x2)dx
=[2x33−2x]√21+[4x−x33]2√2
=(4√23−2√2−23+2)+(8−83−4√2+2√23)
=(203−4√2) sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
The area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣ and y=2 which lies to the right of the line x=1, is
View SolutionArea of the region bounded by the curve y=x2,y=∣∣2−x2∣∣andy=2, which liesto the right of the line x=1, is equal to
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0 and x=3.
View SolutionFind the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionFind the area of the region bounded by the curves y=x2+2y=x,x=0,andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2;y=x;x=0 and x=3
View SolutionFind the area of the region bounded by the curves 2y2=x,3y2=x+1,y=0.
View SolutionFind the area of the region bounded by the curve y=x2and the line y=4.
View SolutionFind the area of the region bounded by the curve y2=4x and x2=4y.
View Solution
