Find the area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣,andyl=2, which lies to the right of the line x=1.Solution in Bengali
The given curves are
y=x2 (1)
y=∣∣2−x2∣∣ (2)
The graphs of these curve are as follows :
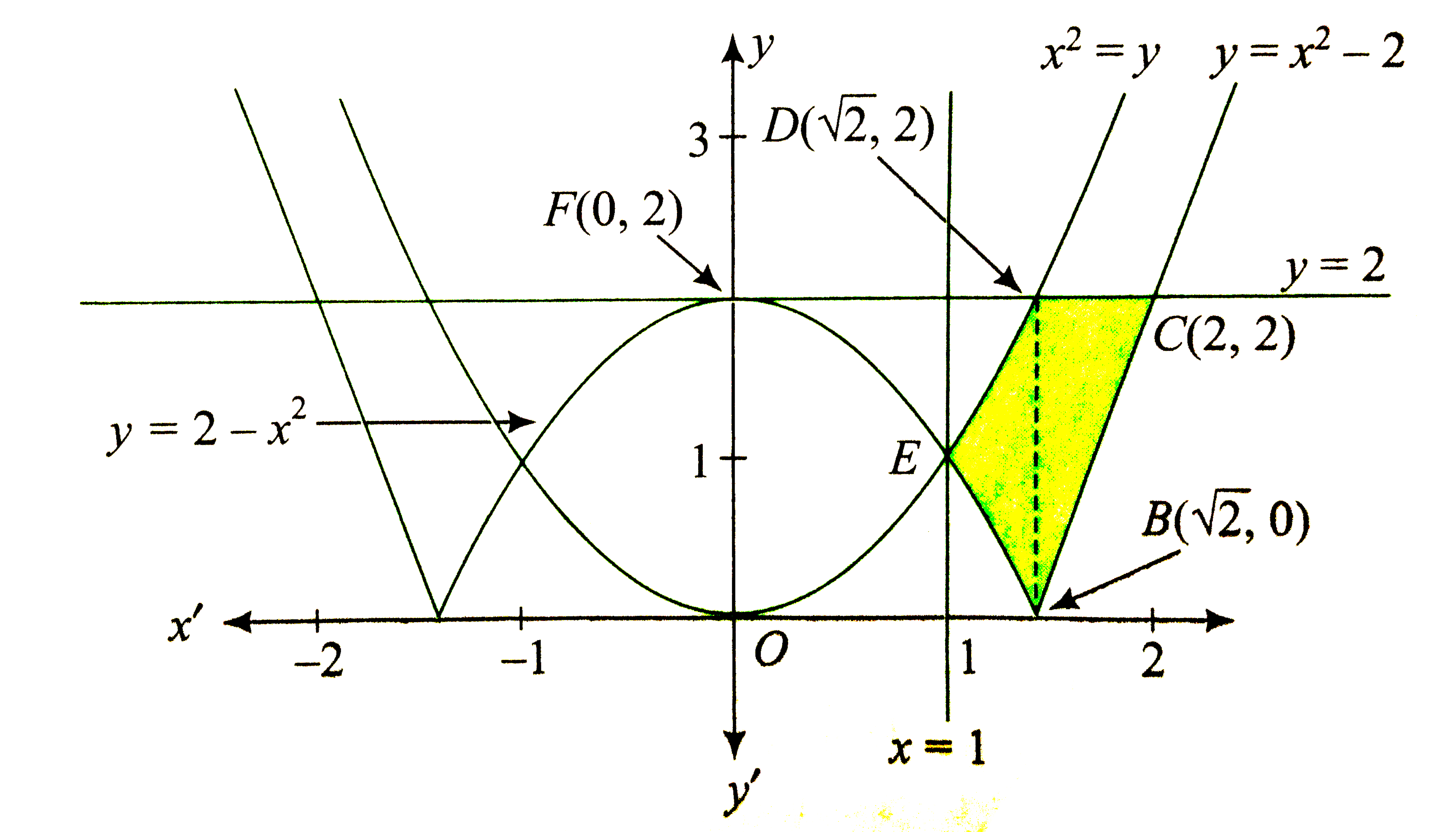
∴ Required area =BCDEB
=∫√21[x2−(2−x2)]dx+∫2√2[2−(x2−2)]dx
=∫√21(2x2−2)dx+∫2√2(4−x2)dx
=[2x33−2x]√21+[4x−x33]2√2
=(4√23−2√2−23+2)+(8−83−4√2+2√23)
=(203−4√2) sq. units.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.214videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
05:57View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
08:04View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then

The function f(x) is02:55View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
10:53View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is04:23View SolutionSketch the curves and identify the region bounded by the curves x=12,x=2,y=logxany=2x. Find the area of this region.
07:55View SolutionArea of the region bounded by the curve y=x^(2),y=|2-x^(2)| and y=2, which liesto the right of the line x=1, is equal to
04:20View SolutionThe area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣ and y=2 which lies to the right of the line x=1, is
02:45View SolutionFind the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
03:29View Solutionवक्र y=x2 तथा रेखा x=1,x=2 एवं X-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
03:00View SolutionSketch the curves and identity the region bounded by x=12,x=2,y=lnx,andy=2x. Find the area of this region.
08:04View SolutionThe area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣ and y=2 which lies to the right of the line x=1, is
02:09View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0,andx=3.
08:21View SolutionSketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
04:49View SolutionFind the area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣,andyl=2, which lies to the right of the line x=1.
05:24View SolutionFind the area bounded by the curve y2=4a2(x−1) and the lines x=1andy=4a.
04:27View Solution

