Find the area of the region bounded by the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

Video Solution

Text Solution

Verified by Experts

The given equation contains only even power of y
So, the cuve is symmetrical about the x-axis.
Also , the given equations contains only even powes of x.
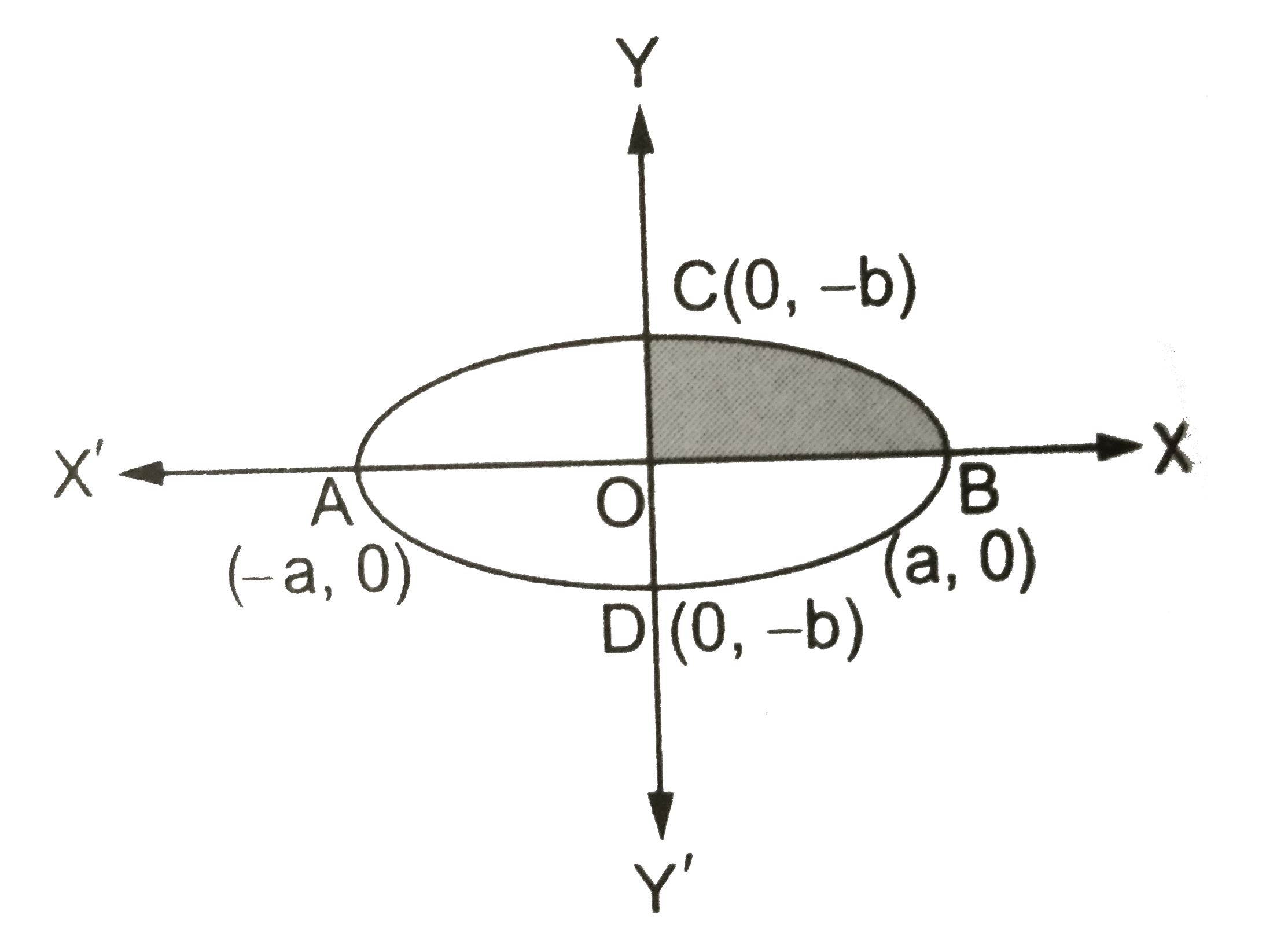
So, the curve is symmetrival about the y-axies ltbgt A rough sketche of the ellipse can be drawn,as showm in the figure .
Now $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \Rightarrow y = \frac{b}{a} . \sqrt{a^{2} - x^{2}}$
Area of the given elliopse
$= 4 \times$ (area OBCO)
$= 4 \times a \int 0 y dx = 4 \times a \int 0 \frac{b}{a} . \sqrt{a^{2} - x^{2}} d x$
$= \frac{4 b}{a} . π / 2 \int 0 a^{2} {cos}^{2} θ d θ$ [ putting x = a sin $θ so that dx =a cos θ d θ]$
$= 4 r^{2} . π / 2 \int 0 \frac{(1 + cos 2 θ)}{2} d θ = (2 a b) . {[θ + \frac{sin 2 θ}{2}]}_{0}^{π / 2}$
$= (π a b)$ sq units
Hence , the area of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 is pi a b$ sq units

Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq units
B $\frac{3 π}{2}$ sq units
C $\frac{5 π}{2}$ sq units
DNone of these
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$