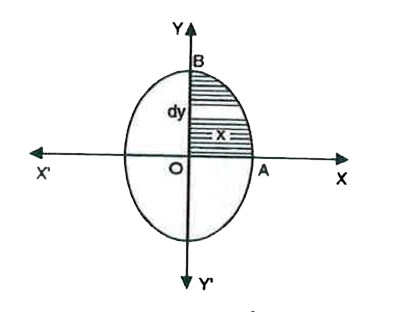
Find the area of the region bounded by the ellipse x2a2+y2b2=1
Video Solution
Text Solution

By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO. Clearly for this region, the limits of integration are 0 and a.
From the equation of the ellipse,
y2b2=1−x2a2=a2−x2a2 ∴y2=b2a2(a2−x2)
In the first quadrant, y>0 ∴y=ba√a2−x2
∴4∫a0ydx=4∫a0ba√a2−x2dx
=4ba∫a0√a2−x2dx
=4ba[x2√a2−x2+a22sin−1(xa)]a0
=4ba[{a2√a2−a2+a22sin−1(1)}−{02√a2−0+a22sin−1(0)}]
=4ba(a22×π2)=πab sq units.
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (2 MARKS )
8 Videos
- APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS ( AREA ) EXERCISE - EXAMPLES FOR PRACTICE (3 OR 4 MARKS )
5 Videos
- APPLICATIONS OF DERIVATIVES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS
12 Videos
Similar Questions
Knowledge Check
Find the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
A3π4 sq unitsB3π2 sq unitsC5π2 sq unitsDNone of theseThe area of the region bounded by the ellipse x225+y216=1 is
A20π sq unitsB20π2 sq unitsC16π2 sq unitsD25π sq unitsThe area of the region bounded by the ellipse x225+y216=1 is
A20π sq unitsB20π2 sq unitsC16π2 sq unitsD25π sq units
Find the area of the region bounded by the curves x=2y−y2 and y=2+x.
View SolutionFind the area of the region bounded by the ellipse :
(a)x29+y24=1
(b)(i)16x2+9y2=144
(ii) 4x2+25y2=1.
View SolutionFind the area of the smaller region bounded by the ellipse x2a2+y2b2=1and the line xa+yb=1
View SolutionFind the area of the region bounded by the ellipse x24+y29=1.
View SolutionFind the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.
View Solution
