Find the area of the region bounded by $x^{2} = 4 y$ , $y = 2, y = 4$ and the $y$ -axis in the first quadrant.

Video Solution

Text Solution

Verified by Experts

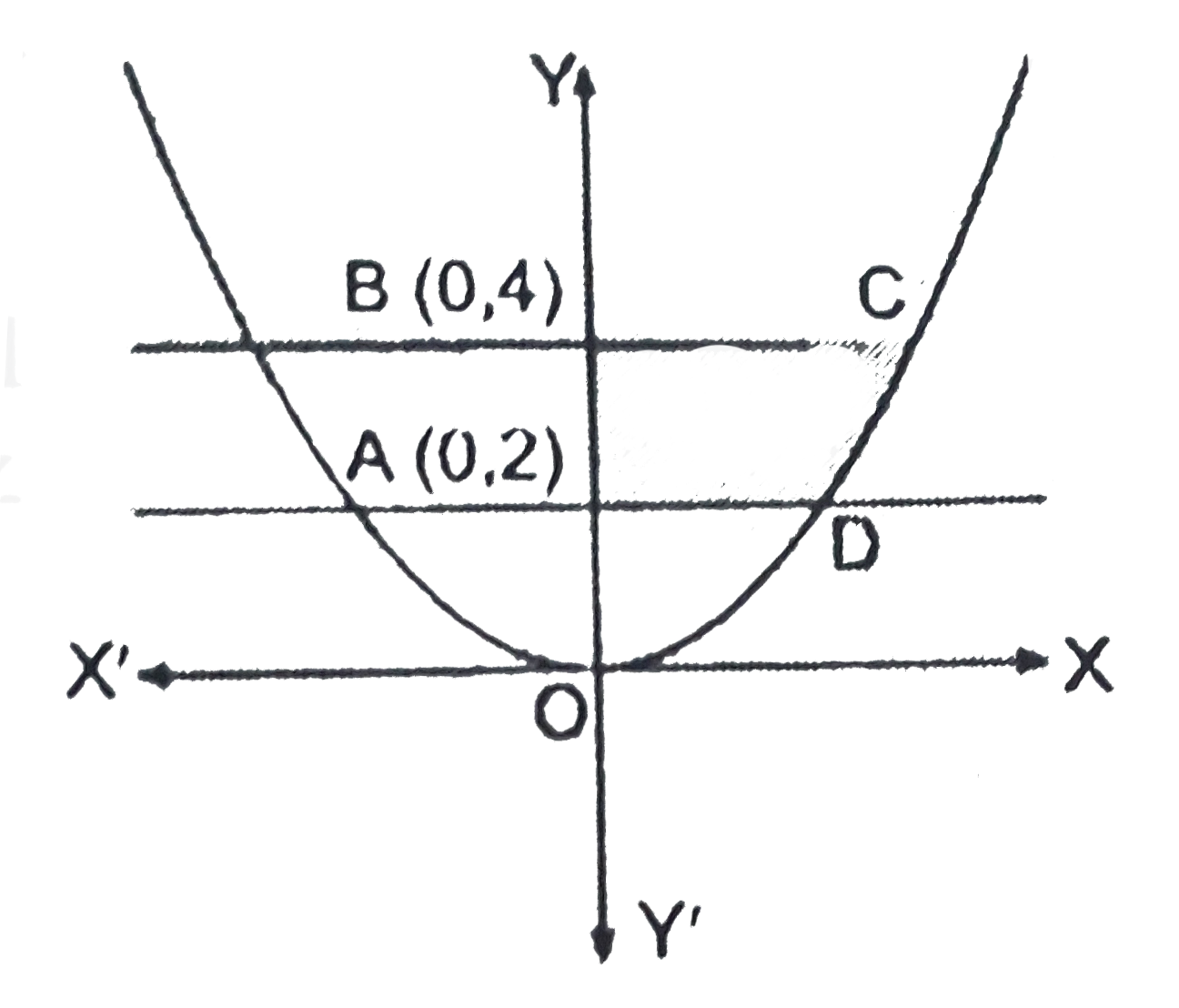
Equation of parabola $x^{2} = 4 y .$
Area of region bounded by $x^{2} = 4 y, y = 2, y = 4$ and Y-axis
$=$ Area of ABCDA
$= \int_{2}^{4} x d y = = \int_{2}^{4} 2 \sqrt{y} d y$
$= 2 . {[\frac{y^{3 / 2}}{3 / 2}]}_{2}^{4} = \frac{4}{3} [4^{3 / 2} - 2^{3 / 2}]$
$= \frac{4}{3} (8 - 2 \sqrt{2}) s q .$ units
$= \frac{8}{3} (4 - \sqrt{2}) s q .$ units

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by $x^{2} = y - 2, y = 4, y = 6$ and the Y-axis in the first quadrant is
A $\frac{2}{3}$
B $\frac{2}{3} (8 - \sqrt{2})$
C $\frac{2}{3} (8 - 2 \sqrt{2})$
D $\frac{3}{2} (8 - \sqrt{2})$
Question 2 - Select One
The area of the region bounded by $x^{2} = 4 y, y = 1, y = 4$ and the y-axis lying in the first quadrant is _________ square units .
A $\frac{22}{3}$
B $\frac{28}{3}$
C $30$
D $\frac{21}{4}$
Question 3 - Select One
The area of the region bounded by $y^{2} = 4 x, x = 0, x = 4$ and the X-axis in the first quadrant is
A16
B $\frac{16}{3}$
C $32$
D $\frac{32}{3}$

NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise

Home
Ask Doubt
Profile