Find the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
The correct Answer is:3 sq. units
Ifx,y>0, then we have
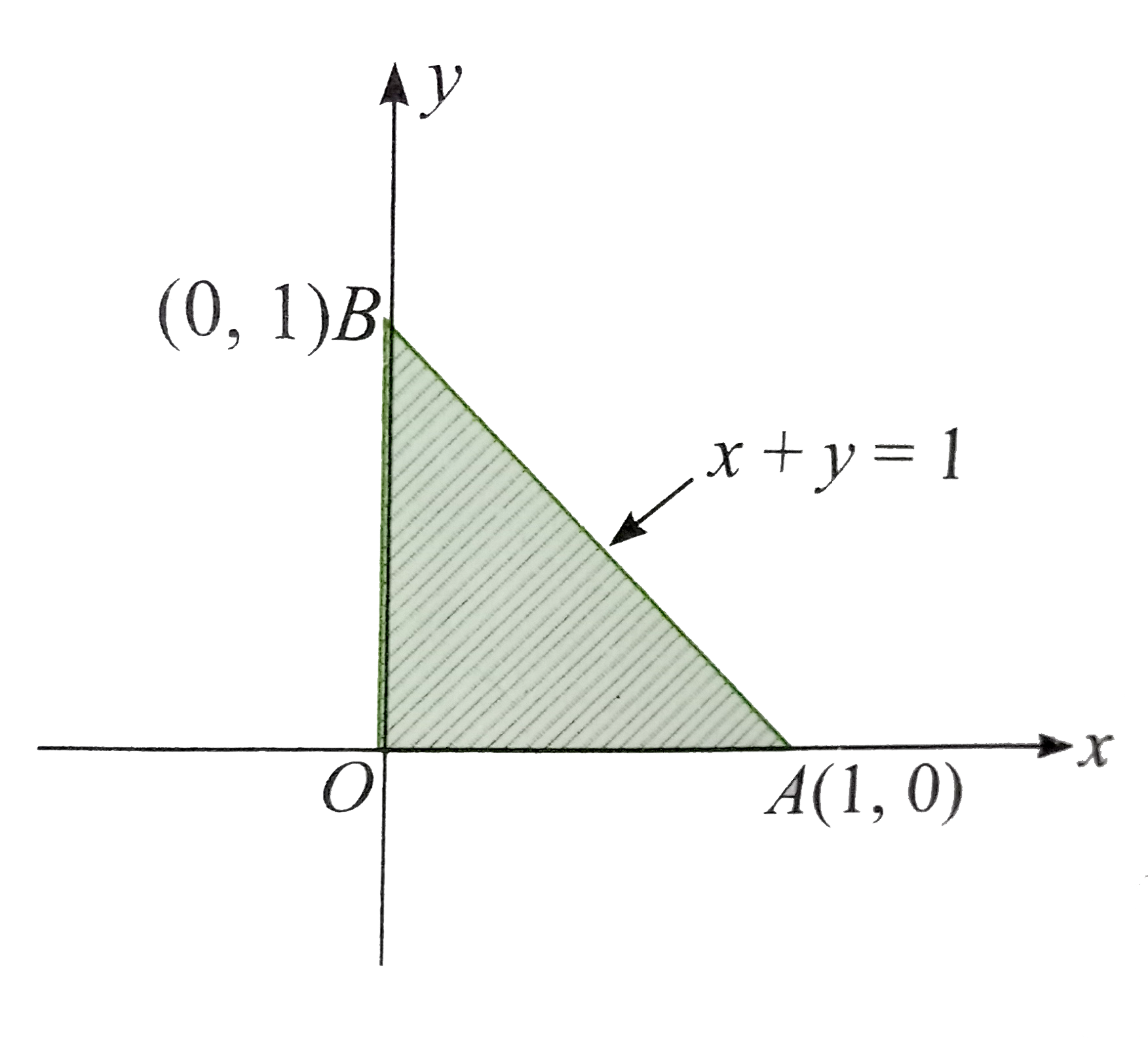
x+y+x+y≤2 or x+y≤1
These inequalities form a triangle region in the first quadrant formed by axes and lines x+y = 1.
Ifx,y<0, then we have
−x−y−x−y≤2 or x+y≥−1
These inequalities form a triangular region in the third quadrant formed by axes and lines x+y=-1.
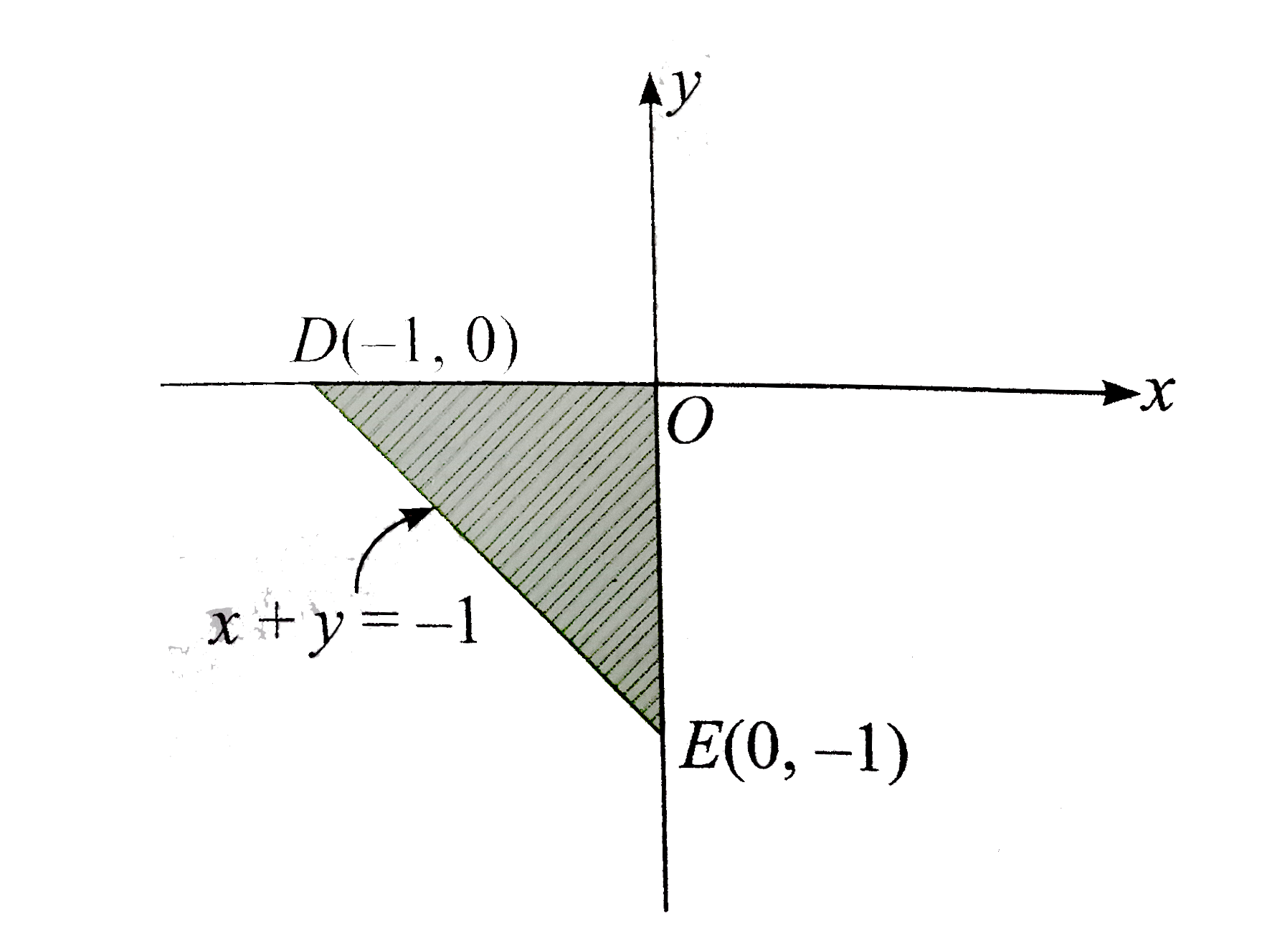
Ifx>0,y<0 and x+y>0, then we have
These inequalities form a triangular region in the fourth quadrant formed by a-axis, a+xy = 0 and x =1.

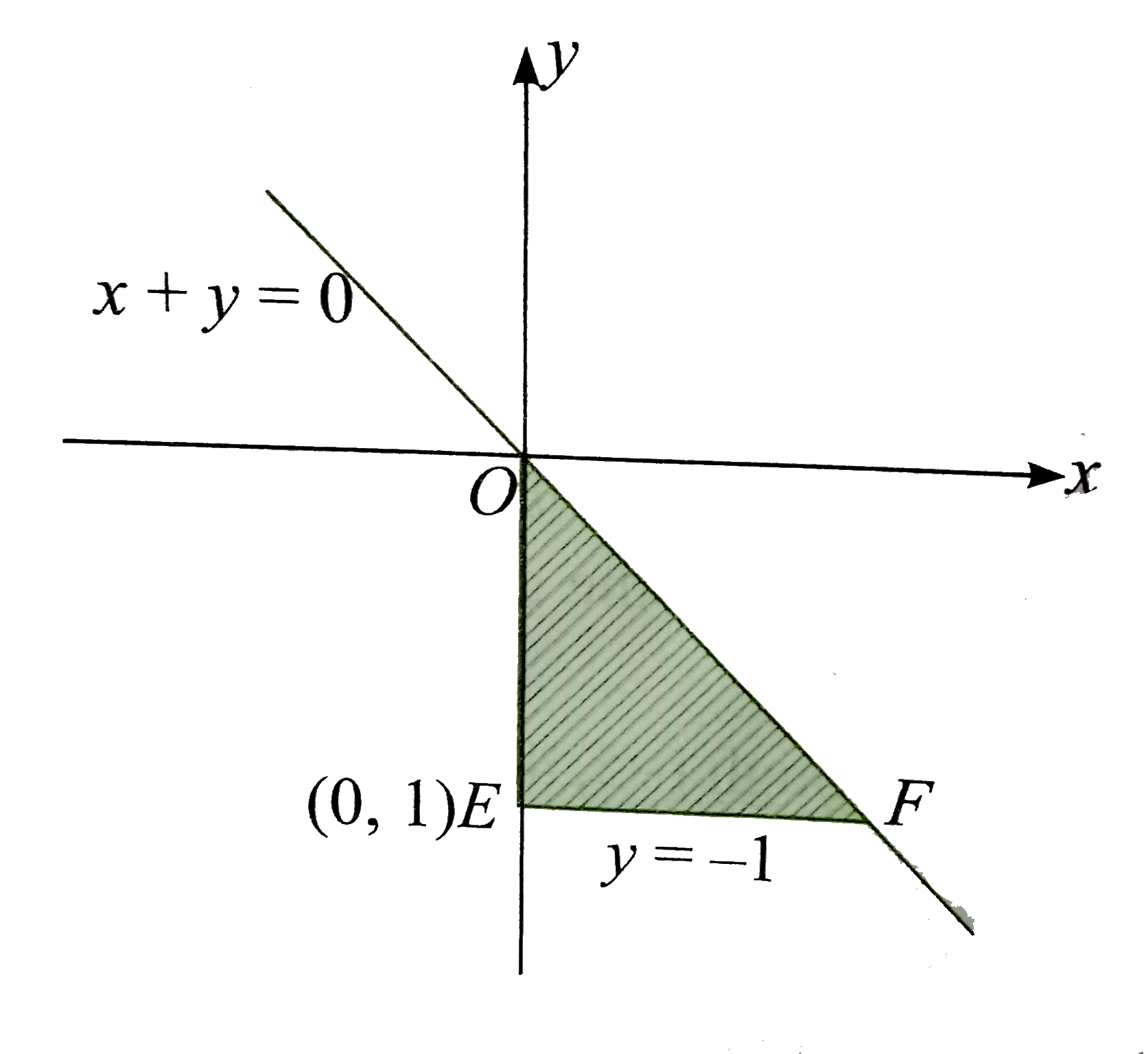
Ifx>0,y<0 and x+y<0, then we have
x−y−x−y≤2 or y≥−1
These inequalities form a trianglular region in the fourth quadrant formed by y-axis, x+y = 0 and y=-1
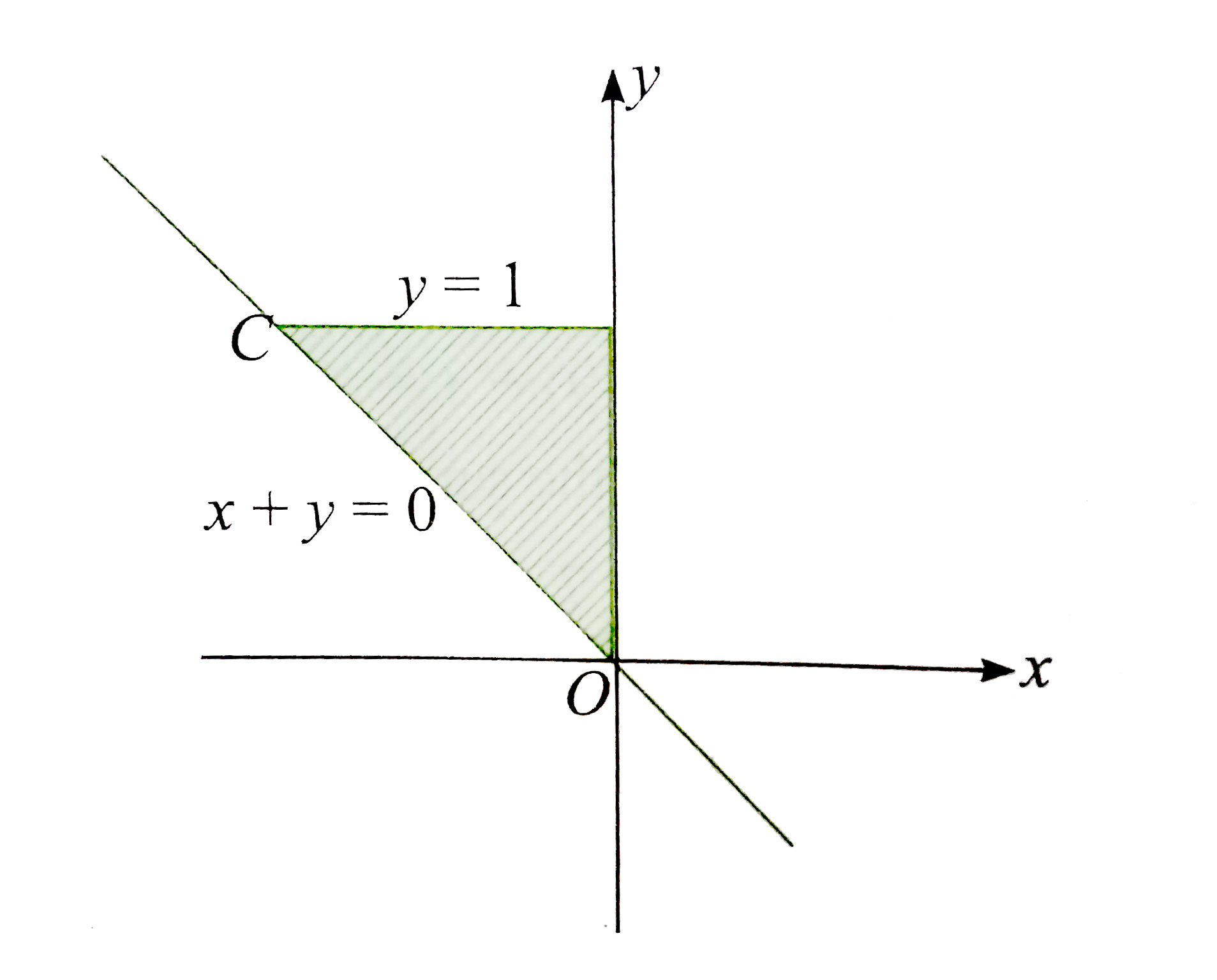
Ifx<0,y>0 and x+y>0, then we have
−x+y+x+y≤2 or y≤1
These inequalities form a triangular region in the second quadrant formed by y-axis, x+y = 0 and y=1.
Ifx<0,y>0 and x+y<0, then we have
−x+y−x−y≤2 or x≥−1
These inequalities form a triangular region in the second quadrant formed by x-axis, x+y=0 and x =-1.
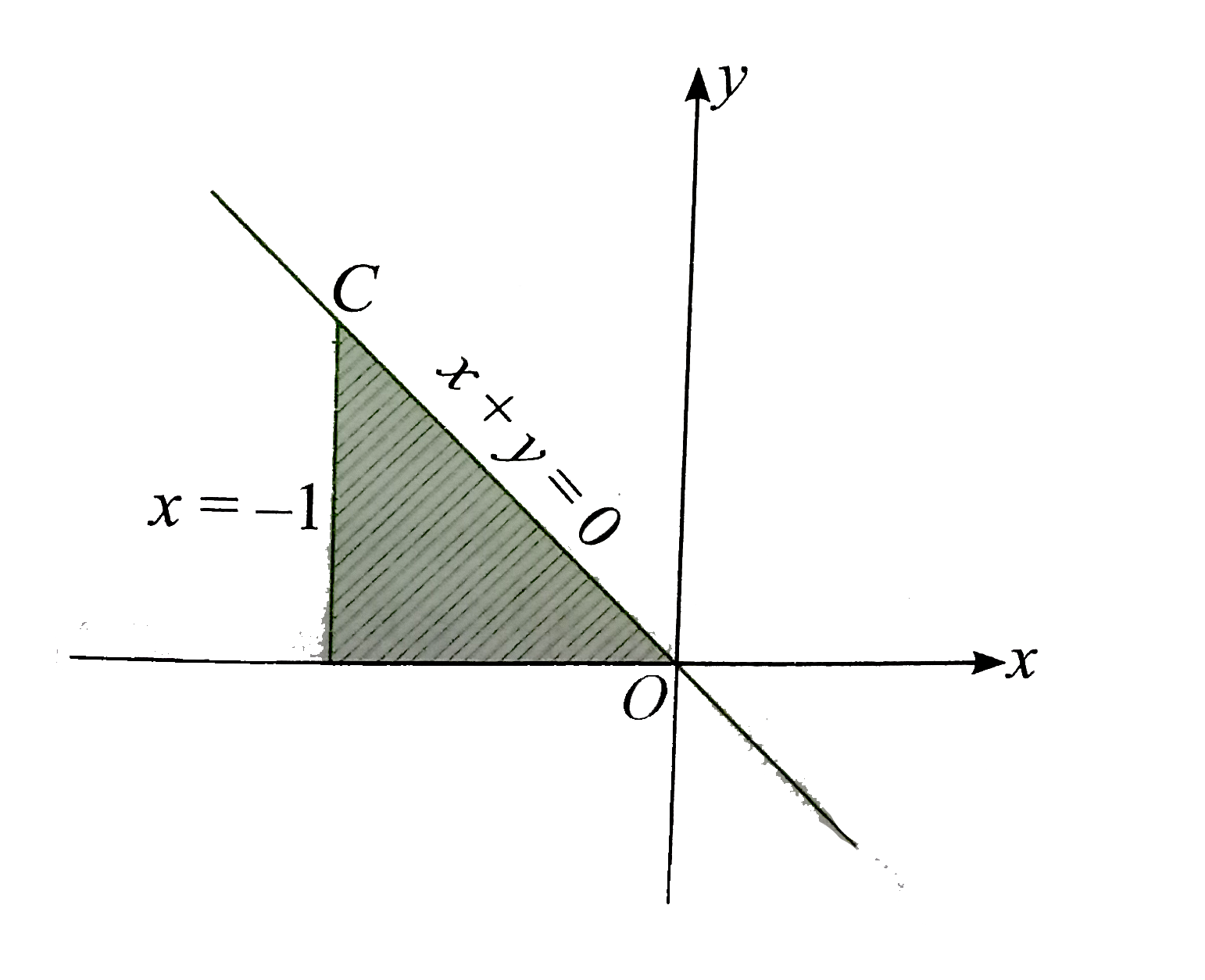
Combining all the regions, we have following region in the plane
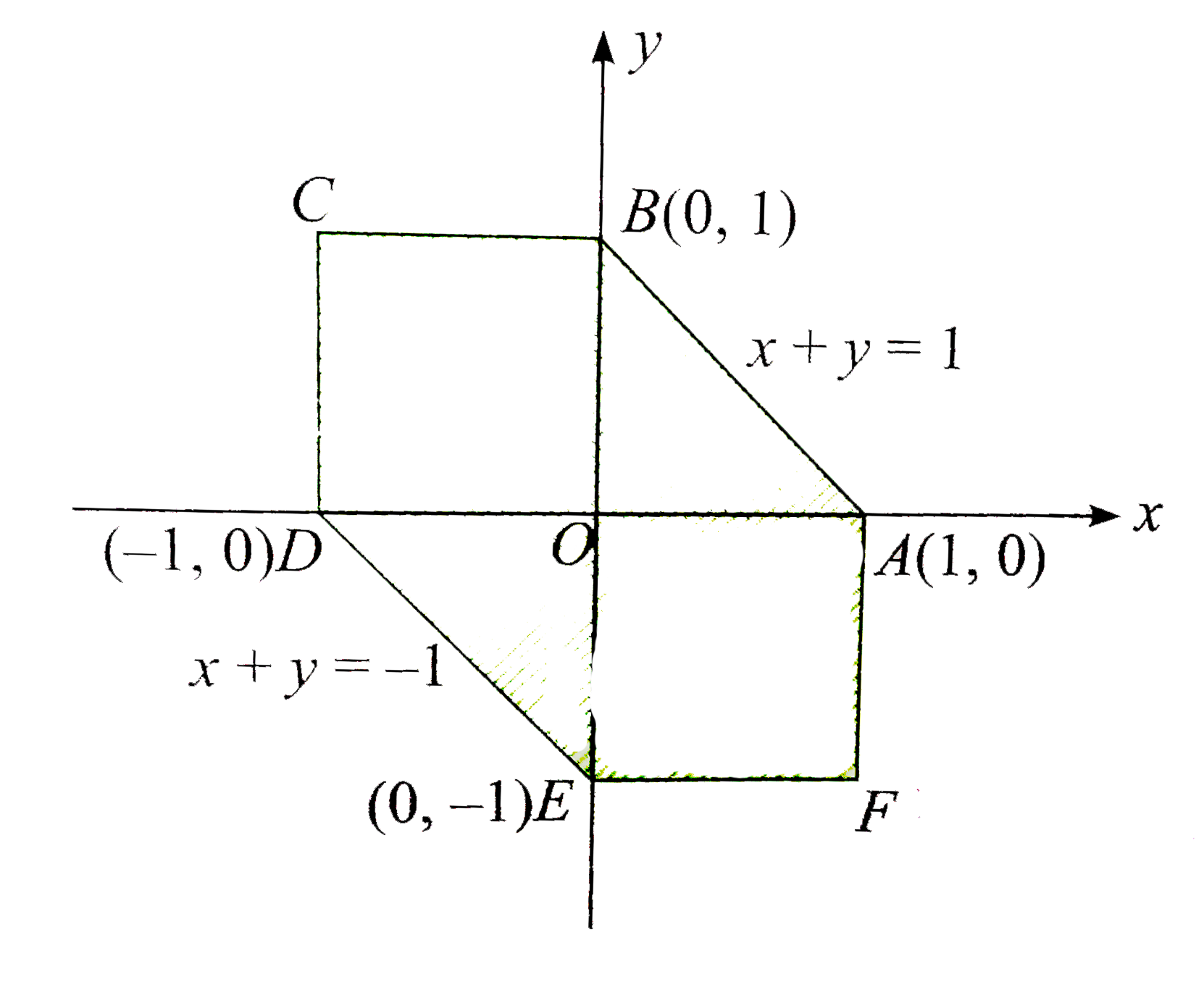
Area of the above region =3× Area of square having side length 1 unit.
= 3 sq. unit.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.58videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.37videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Find the area of the region in which points satisfy
3≤|x|+|y|≤5.View SolutionFind the area of the region in which points satisfy
3≤|x|+|y|≤5.View SolutionSketch the region of the points satisfying max.{|x|,|y|}≤4.
View SolutionSketch the region of the points satisfying max.{|x|,|y|}≤4.
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region {(x,y):x2≤y≤x}
View SolutionFind the area of the region [ (x,y):x2≤y≤x)
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View SolutionFind the area of the region given by :
{(x,y):x2≤y≤|x|}.
(ii) Find the area bounded by thte curves :
{(x,y):y≥x2andy=|x|}.
(iii) Find the area of the region bounded by the parabola y=x2andy=|x|.View Solution
