Find the area of the region in the first quadrant enclosed by the y-axis, the line y=x and the circle x2+y2=32, using integration.
16π sq units
4π sq units
32π sq units
24π sq units
The correct Answer is:B
We have, area enclosed by X-axis i.e., y = 0, y = x and the circle x2+y2=32 in first quadrent.
Since, x2+(x)2=32[∵y=x]
⇒22=32
⇒x=±4
So, the intersection point of circle x2+y2=32 and line y=x are (4,4) or (−4,4).
and x2+y2=(4√2)2
Since, y=0
∴x2+(0)2=32
⇒x=±4√2
So, the circle intersects the X-axis at (±4√2,0).
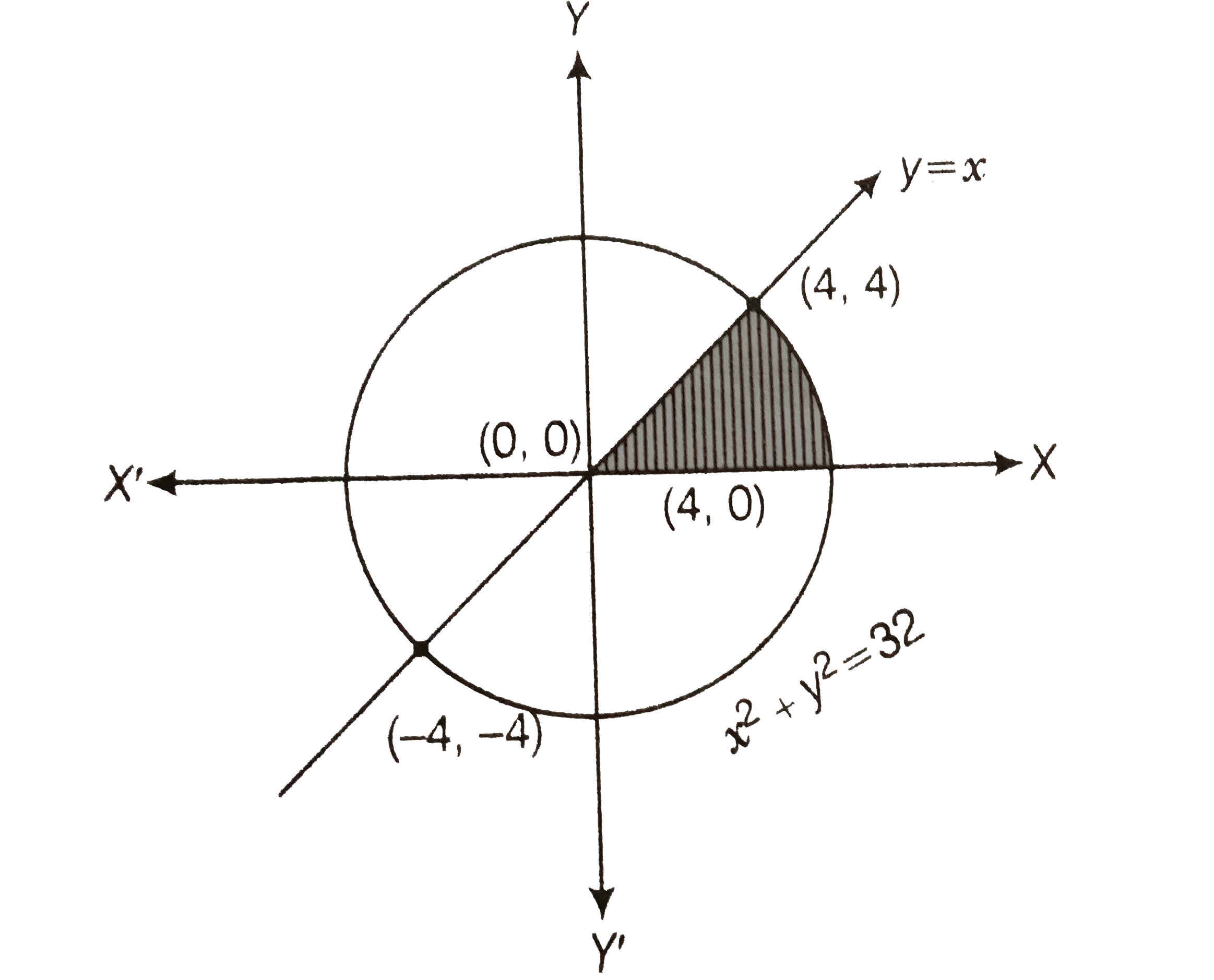
Area of shaded region =4∫0xdx+4√2∫4√(4√2)2−x2dx
=∣∣∣x22∣∣∣40+∣∣
∣
∣∣x2√(4√2)2−x2+(4√2)22sin−1.x4√2∣∣
∣
∣∣4√24
=162+⎡⎢
⎢⎣4√22.0+16sin−1.(4√2)(4√2)−42√(4√2)2−16−16sin−1.44√2⎤⎥
⎥⎦
=8+[16.π2−2.√16−16.π4]
=8+[8π−8−4π]=4π sq units
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Long Answer Type Questions
16 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers
5 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - True/False
10 Videos
Similar Questions
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x , and the circle x2+y2=32 .
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionFind the area of the region in the first quadrant enclosed by x-axis, the line y=√3 x and the circle x2+y2=16
View SolutionFind the area of the region in the first quadrant enclosed by x-axis, line x=√3yand the circle x2+y2=4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1andy=4.
View SolutionFind the area of the region enclosed by the parabola x2=y , the line y = x + 2 and the x-axis.
View SolutionThe plumule of wheat is enclosed in
View SolutionFind the area of the region enclosed by the curve y=∣∣∣x−1x∣∣∣(x>0) and the line y=2
View SolutionFind the area of region bounded by the curve ay2=x3, the y-axis and the lines y=aandy=2a.
View SolutionThe area (in sq. units) of the region in the first quadrant bounded by y=x2,y=2x+3 and the y - axis is
View Solution
