Find the area of the region in which points satisfy
$3 \leq | x | + | y | \leq 5 .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:32 sq. units

We have $3 \leq | x | + | y | \leq 5$ .
$| x | + | y | \leq 5$ means that points lie inside the square endpoints of whose diagonal are $(\pm 5, 0) and (0, \pm 5) .$
$| x | + | y | \geq 3$ means that points lie outside the square endpoints of whose diagonal are $(\pm 3, 0) and (0, \pm 3) .$
So, common region is as shown in the figure.

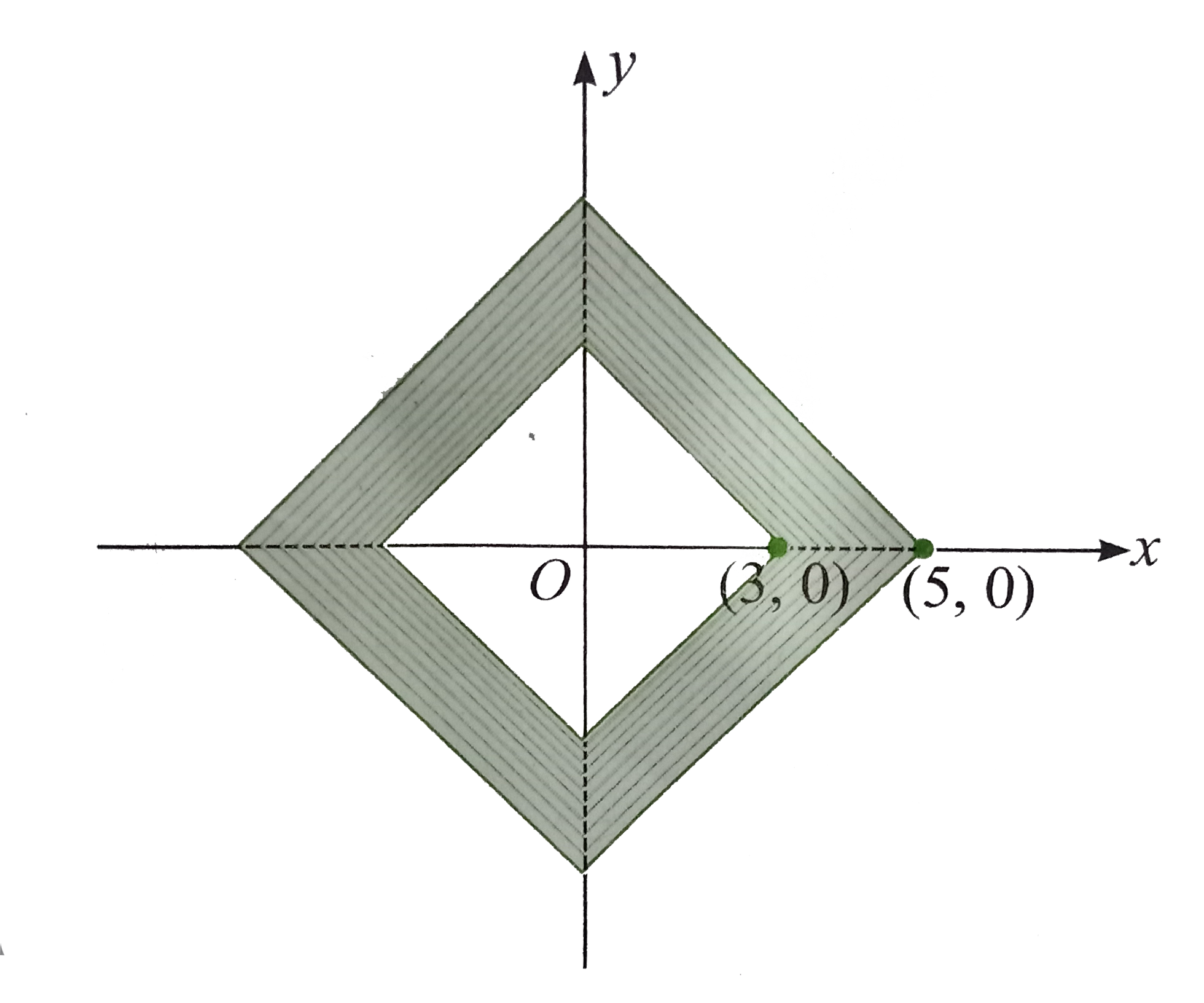
$Area of region = 4 (\frac{1}{2} \times 5 \times 5 - \frac{1}{2} \times 3 \times 3) = 32 sq.units$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region on place bounded by max $(| x |, | y |) \leq \frac{1}{2}$ is
A $1 / 2 + ln 2$
B $3 + ln 2$
C $31 / 4$
D $1 + 2 ln 2$

CENGAGE-STRAIGHT LINES-Exercise 2.4

Home
Ask Doubt
Profile