Find the area of the smaller region bounded by the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ and the line $\frac{x}{a} + \frac{y}{b} = 1$

Video Solution

Text Solution

Verified by Experts

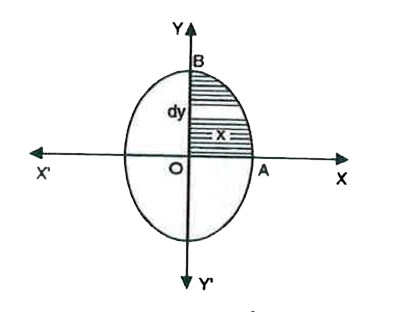
The ellopse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ and the
line $\frac{x}{a} + \frac{y}{b} = 1$ can be drawn as shown in the given figure
Then , we have of the area of the shaded region
Required area
= {area between $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ and the x-axis from x=0 to x=a }
- {area between the line $\frac{x}{a} + \frac{y}{b} = 1$ and the x-axis from x=0 to x =a }
$= a \int 0 (y of the ellipse) d x - a \int 0 (y of the line x) d x$
$a \int 0 \frac{b}{a} . \sqrt{a^{2} - x 2} d x - a \int 0 \frac{b (a - x)}{a} d x$
$= \frac{b}{a} . {⎡ ⎢ ⎢ ⎣ \frac{x (\sqrt{a^{2} - x^{2}})}{2} + \frac{a^{2}}{2} {sin}^{- 1} \frac{x}{a} ⎤ ⎥ ⎥ ⎦}_{0}^{a} - \frac{b}{a} . {[a x - \frac{x^{2}}{2}]}_{0}^{a}$
$= \frac{a b}{a} ({sin}^{- 1} 1 - {sin}^{- 1} 0) - (a b - \frac{a b}{2}) = (\frac{π a b}{4} - \frac{a b}{2})$ sq units
Hence , the required area is $(\frac{π a b}{4} - \frac{a b}{2})$ sq units.

Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

A $10 π$
B $11 π$
C $12 π$
D $13 π$
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$