Find the area under the curve y=√x−1 in the interval [1, 5] between the lines x = 1 and x = 5, is
A
43 sq units
B
83 sq units
C
163 sq units
D
None of the above
Video Solution
Text Solution
The correct Answer is:C
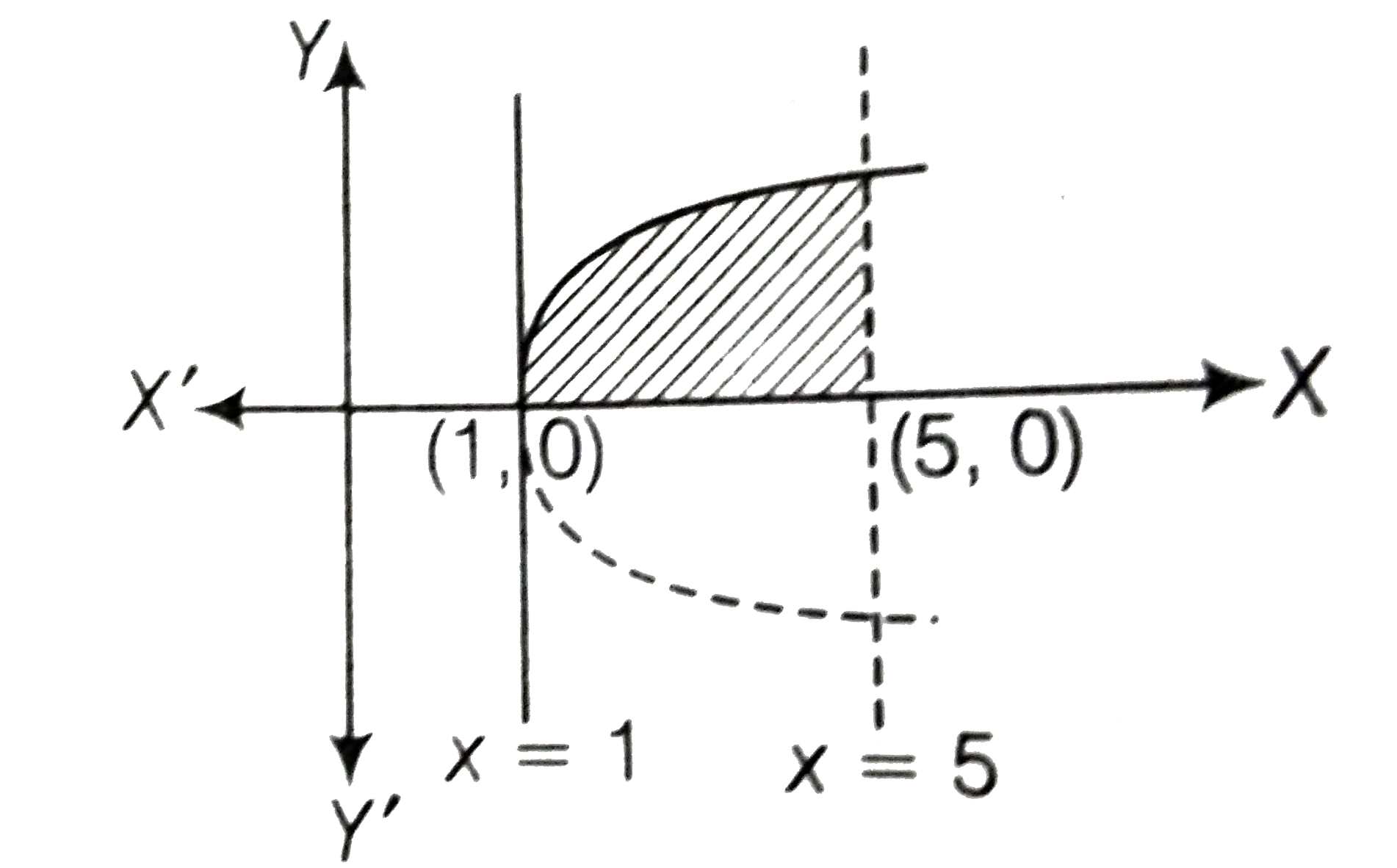
∴ Required area (shown in shaded region)
=∫51ydx=∫51√x−1dx=[2(x−1)3/23]51
=23[(5−1)3/2−(1−1)3/2]
=23[(4)3/2]=163 sq units
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
What is the area under the curve f(x)=xex above the X-axis and between the lines x=0 and x=1?
A12 sq. unitB1 sq unitC32 sq. unitsD2 sq. units
Find the area under the curve y=2√x between the ordinates y=0andx=1.
View SolutionDetermine the area under the curve y=√a2−x2 included between the lines x=0andx=a.
View SolutionCalculate the area under the curve y=2√x included between the lines x = 0 and x = 1.
View SolutionCalculate the area under the curve y=2√x included between the lines x = 0 and x = 1.
View SolutionFind the area of the region bounded by the curve y=x2 , the x-axis, and the lines x = 1 and x = 3.
View SolutionFind the area bounded by the curves y=x+√x2andxy=1, the x-axis and the line x=2.
View SolutionDraw a rough sketch of the curve y=√x−1) in the interval [1, 5]. Find the area under the curve and between the lines x = 1 and x = 5.
View Solution
