The area bounded by the curves y = x , 2 y - x + 3 = 0 , X-axis and lying in the first quadrant is

A

9

B

36

C

18

D

27 4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Given curves are y = x ... (i)
and 2 y - x + 3 = 0 ... (ii)
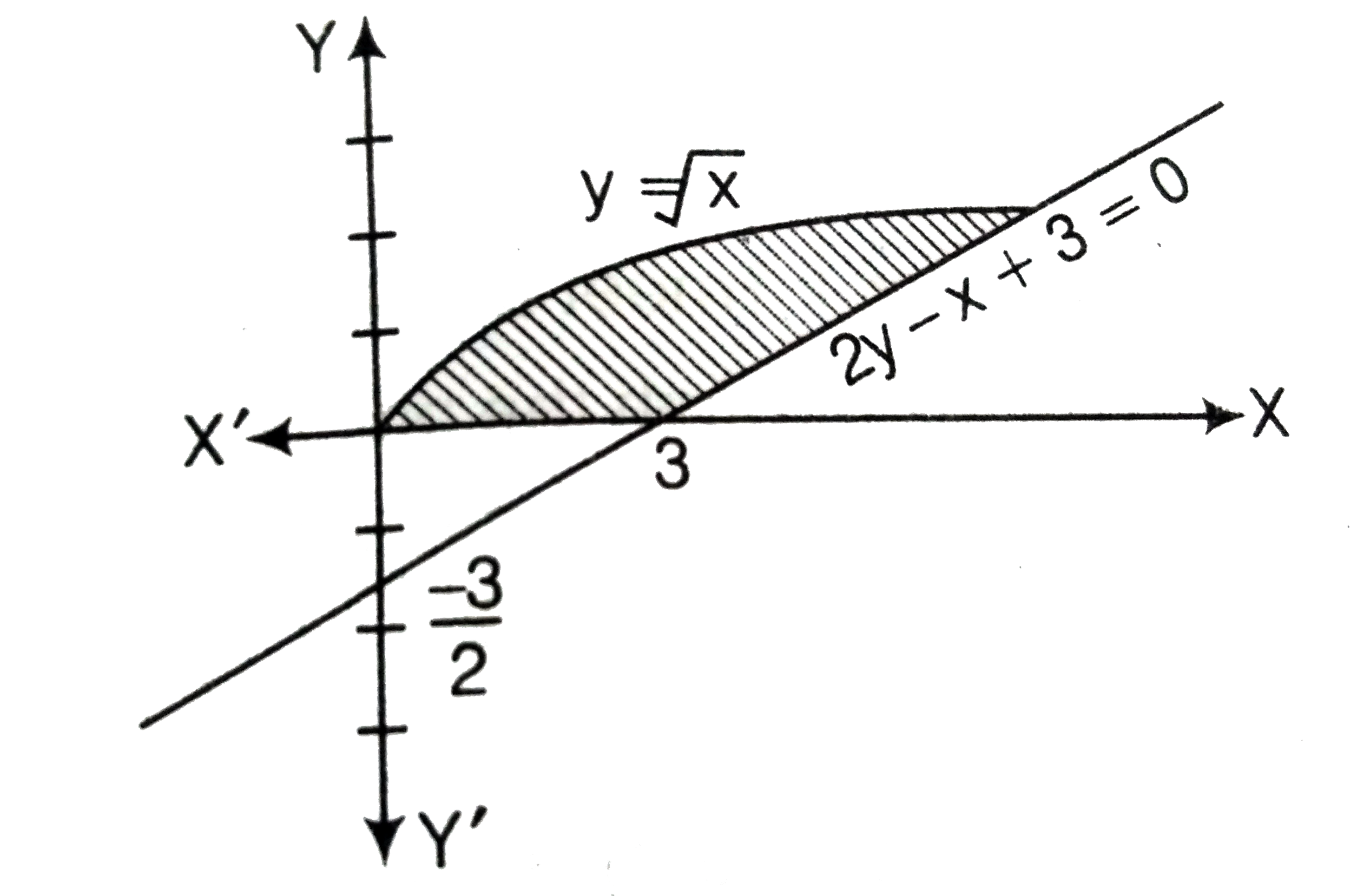
ocr_image
On solving Eqs. (i) and (ii), we get
2 x - ( x ) 2 + 3 = 0
⇒ ( x ) 2 - 2 x - 3 = 0
⇒ ( x - 3 ) ( x + 1 ) = 0
⇒ x = 3 , [ ∵ x = - 1 is not possible]
∴ y = 3
∴ REquired area = ∫ 0 3 ( x 2 - x 1 ) d y
= ∫ 0 3 { ( 2 y + 3 ) - y 2 } d y
= [ y 2 + 3 y - y 3 3 ] 0 3
= 9 + 9 - 9 = 9

Updated on:21/07/2023
|
Class 12MATHSAPPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The area (in square units) bounded by the curves y=√x,2y−x+3=0, x-axis, and lying in the first quadrant is

    A9
    B36
    C18
    D274

  • The area (in square units) bounded by the curves y=√x,2y−x+3=0, x-axis, and lying in the first quadrant is

    A9
    B36
    C18
    D274

  • The area bounded by the curve y=sin2x, axis and y=1, is

    A1
    B1/4
    Cπ/4
    Dπ/4−1/2